Straight lines coordinate geometry
Lines are drawn through point P parallel to the sides of triangle A B C . The resulting 3 triangles have areas 4, 9, and 49.
What is the area of triangle A B C ?
The areas of these 3 smaller triangles are 4, 9, and 49. What's the area of the big, outer triangle?
The answer is 144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
I thought to start this way too.
Sorry but why the ratio of the sides must be 2:3:7?
Log in to reply
Because for similar figures, the ratio of the areas is always the square of the ratio of the sides
what do u do
translating the blue triangle to the top of the bigger triangle makes it visually easier to solve yellow : red : blue : large = 2 : 7 : 3 : 1 2 ( 2 + 7 + 3 = 1 2 ) .
Since the 3 resulting triangles are made from parallel sides, their angles are congruent, which means they are all similar to each other and △ A B C by AA similarity. Let b 1 be the base of the triangle with area 4 , b 2 the base of the triangle with area 9 , and b 3 the base of the triangle with area 4 9 .
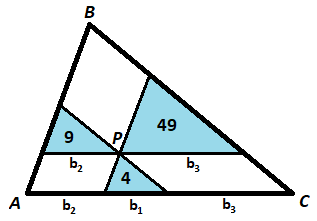
The ratio of the sides of similar triangles is the square root of the ratio of the areas. Therefore, b 3 b 1 = 4 9 4 = 7 2 and b 3 b 2 = 4 9 9 = 7 3 , which means b 1 = 7 2 b 3 , and b 2 = 7 3 b 3 .
The base of △ A B C is equivalent to b 1 + b 2 + b 3 , which is 7 2 b 3 + 7 3 b 3 + b 3 = 7 1 2 b 3 .
This means that the ratio of the sides of △ A B C and the sides of the triangle with the area of 4 9 is b 3 7 1 2 b 3 = 7 1 2 .
Since the ratio of the areas is the square of the ratio of the sides, the area of △ A B C is 7 2 1 2 2 ⋅ 4 9 = 1 4 4 .
The triangles are similar, so the ratio of corresponding sides is red : yellow : blue = 7 : 2 : 3 . Consider the side at the bottom of each triangle. Translating the blue triangle to the bottom left along A B and the red triangle to the bottom right along B C shows that A C = side of large triangle = blue side + yellow side + red side , so that the side ratios become red : yellow : blue : large = 7 : 2 : 3 : 1 2 ( 7 + 2 + 3 = 1 2 ) . The ratio of areas is therefore red : yellow : blue : large = 4 9 : 4 : 9 : 1 4 4 .
Oh this is just beautiful! I'm speechless by its simplicity! Thanks for sharing.
The triangles are similar
This is amazing method to define the answer
The triangles are all similar so the ratio of the areas is proportional to the square proportion of the side lengths. The side lengths blue:yellow:red:ABC are then in the extended proportion 3:2:7:12 so the area is 1 2 2 = 1 4 4
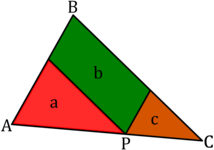
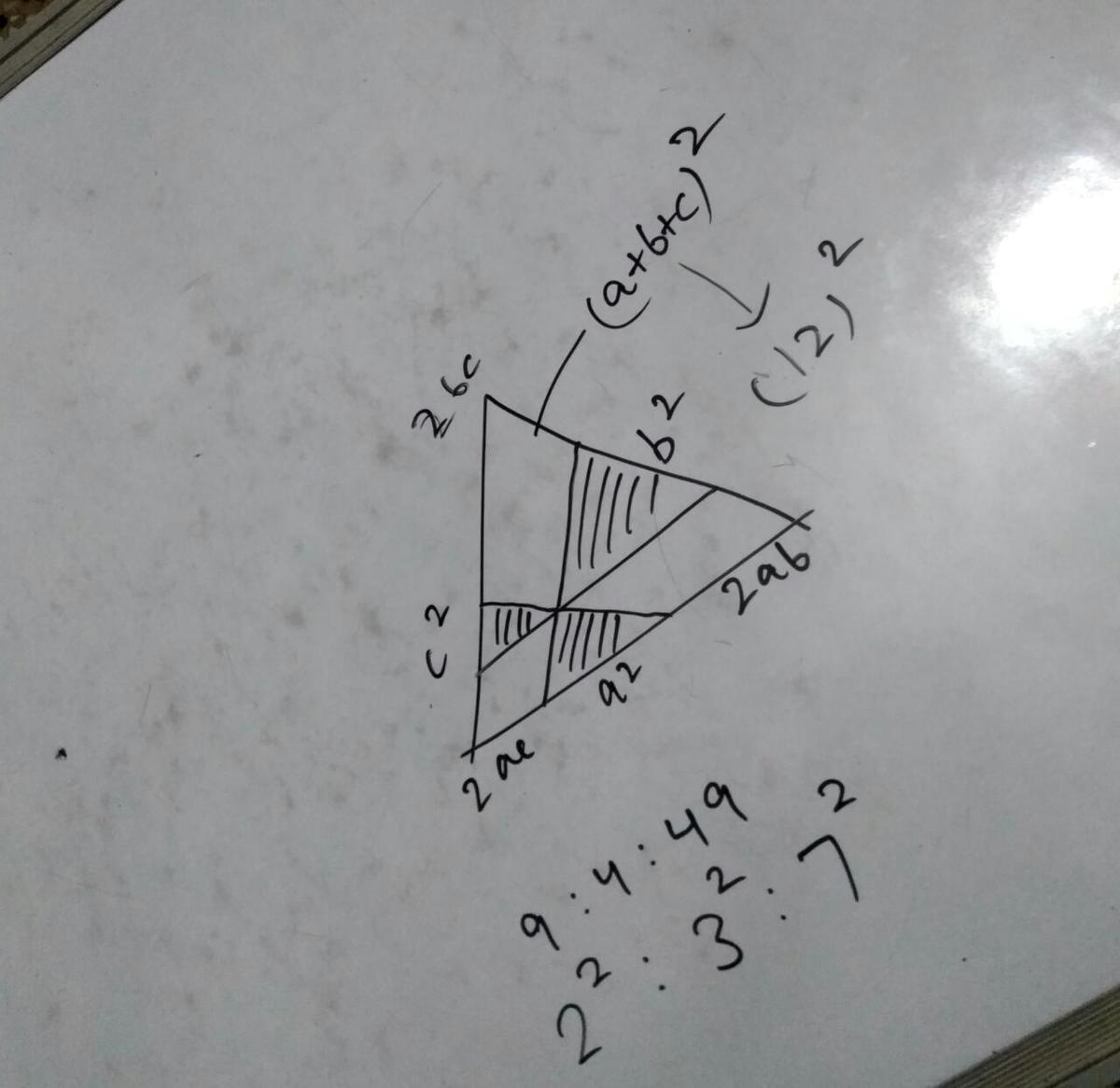
Lemma: Given a triangle A B C and a point P on the side A C if we trace the parallels to each other side of the triangle passing through P and label the resulting areas as in the figure then b 2 = 4 a c
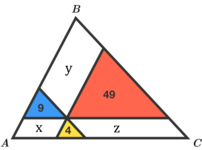
Now we use the lemma on the triangle of the problem
- x 2 = 4 ⋅ 4 ⋅ 9 then x = 2 ⋅ 2 ⋅ 3 = 1 2 .
- y 2 = 4 ⋅ 9 ⋅ 4 9 then y = 2 ⋅ 3 ⋅ 7 = 4 2 .
- z 2 = 4 ⋅ 4 9 ⋅ 4 then z = 2 ⋅ 7 ⋅ 2 = 2 8 .
Then the area of the whole triangle is Area = x + 9 + y + 4 9 + z + 4 = 1 4 4
Note: The proof of the lemma is a fun puzzle on itself, I'll leave it in case someone wants to try :)
I for one would like to see proof, please.
You can shift the blue triangle up, the yellow triangle right, mirror this at BC and then have areas 18, 98, and 8. Then you can skew and resize the parallelogram to a rectangle and finally a square with same areas and ratios as before and the overall area then is the solution:
You get to the same conclusion from this, the overall area is 12x12=144
My slightly off-kilter solution used some tricks and assumptions.
Notice that you can "slide" the blue and red triangles down the sides of the yellow triangle, exactly filling the larger base with their three smaller bases.
Notice that 4, 9 and 49 are perfect squares, so maybe the square roots are useful (otherwise the question setter would probably have used different numbers).
Now, pretend that they ARE squares instead of triangles. So their sides are the square roots of their areas, ie 2, 3 and 7.
Add these up to get the side of our pretend larger square, which is 12.
The area of a square of size 12 is 144.
I think this works because I've made several unwarranted assumptions which all happen to cancel out. Perhaps somebody better at geometry could show why.
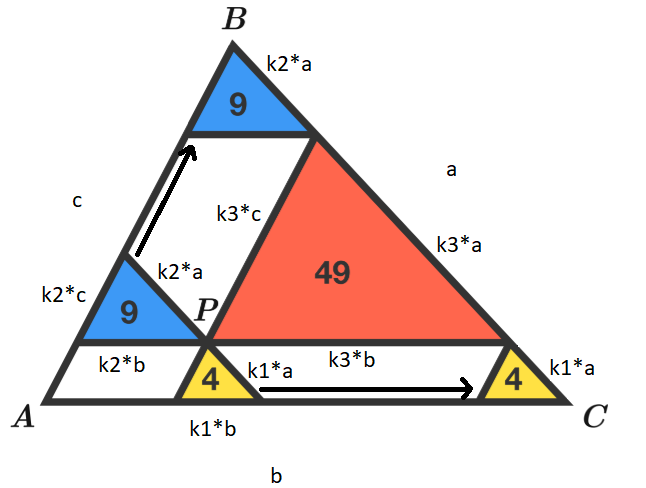
Since the lines through point P are drawn parallel to the sides of triangle ABC, we can conclude that the new triangles are similar to triangle ABC (in other words, they have the same shape). With this, the sides of every new triangle are the sides of triangle ABC multiplied by a constant (I prefer to use k 1 , k 2 , k 3 , k 1 for the tiniest of the new triangles, etc.) See picture below. The areas of the new triangles are dependent on the squares of the constant the sides of that particular triangle were multiplied with. This means that k 1 2 ∼ 4 , k 2 2 ∼ 9 , k 3 2 ∼ 4 9 , which implies that k 1 : k 2 : k 3 = 2 : 3 : 7 (the constants cannot be negative).
If you drag all the new triangles to one side of triangle ABC, you will notice that they fit perfectly on that side, which implies that k 1 + k 2 + k 3 = 1 . With those two conditions for the constants, we can calculate the values of them. k 1 = 2 + 3 + 7 2 = 6 1 , k 2 = 2 + 3 + 7 3 = 4 1 , k 3 = 2 + 3 + 7 7 = 1 2 7
If you multiply only the base (doesn't really matter which of the sides you choose, just use the same for the three triangles) of the three smaller (new) triangles) by the reciprocal of respectively k 1 , k 2 , k 3 , you will end up with one base b. The heights of the three individual triangles are unknown. However, because the heights of the three individual triangles added together are exactly the height of triangle ABC, if you add the area of the three triangles with the same base (but different heights) you will end up with the area of triangle ABC. So the area of triangle ABC is equal to 4 k 1 − 1 + 9 k 2 − 1 + 4 9 k 3 − 1 = 4 ⋅ 6 + 9 ⋅ 4 + 4 9 ⋅ 7 1 2 = 1 4 4
How do you know the sum of the two triangles and the parallelogram.
UNHELPFUL SOLUTION HERE
I first spent time working with the fact that they are similar triangles, and each side of the large triangle is the sum of the corresponding sides of the small ones, and then used Herons formula to connect that information. Then I gave up and imagined filling up the big triangle with the others and got the answer of 144 with my first guess. Not a very helpful solution, I know, but hopefully amusing.
x^2sin(60) = 18, y^2sin(60) = 98, z^2sin(60) = 8 , x + y + z = BC, 1/2sin(60)(x + y + z)^2 = 144. x = sqrt(18/sin60) y = sqrt(98/sin(60)) z = sqrt(8/sin(60))
2 plus 2 is 4 times 3 is 12 square is 144 intermediate speed math
Define points E and F as the points on BC where the parallel lines intersect BC. The triangles whose area are 4,9,49, and |ABC| are similar, having angles respectively equal y parallelism. Let FC = x. then EF/FC = sqrt(49/4) = 7/2. So EF = (7/2)x. BE/EF = sqrt(9/49) = 3/7, so BE = (3/7)(EF) = (3/2)x. Then BC = BE + EF + FC = 6x. Finally, 49/|ABC| = [(EF)^2]/[(BC)^2)] =([49/4) x^2]/[36 x^2] = 49/144, so |ABC| = 144. Ed Gray
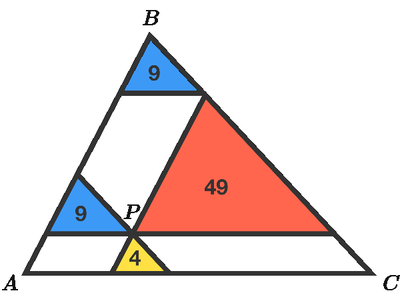 We note that smaller yellow, blue and red triangles of areas 4, 9 and 49 respectively are similar to
△
A
B
C
.
We note that smaller yellow, blue and red triangles of areas 4, 9 and 49 respectively are similar to
△
A
B
C
.
For similar triangles the linear dimensions (height and base) are directly proportional to the square root of the area. Therefore, h y : h b : h r = b y : b b : b r = 4 : 9 : 4 9 = 2 : 3 : 7 . If h y = 2 , then h b = 3 and h r = 7 .
By stacking the blue triangle on top of the red triangle as shown in the figure, we see that the height of △ A B C is h A B C = h y + h b + h r = 2 + 3 + 7 = 1 2 .
Since area is proportional the squared of linear dimension, then the area of △ A B C , A y A A B C = 2 2 1 2 2 ⟹ A A B C = 4 1 4 4 A y = 1 4 4 .
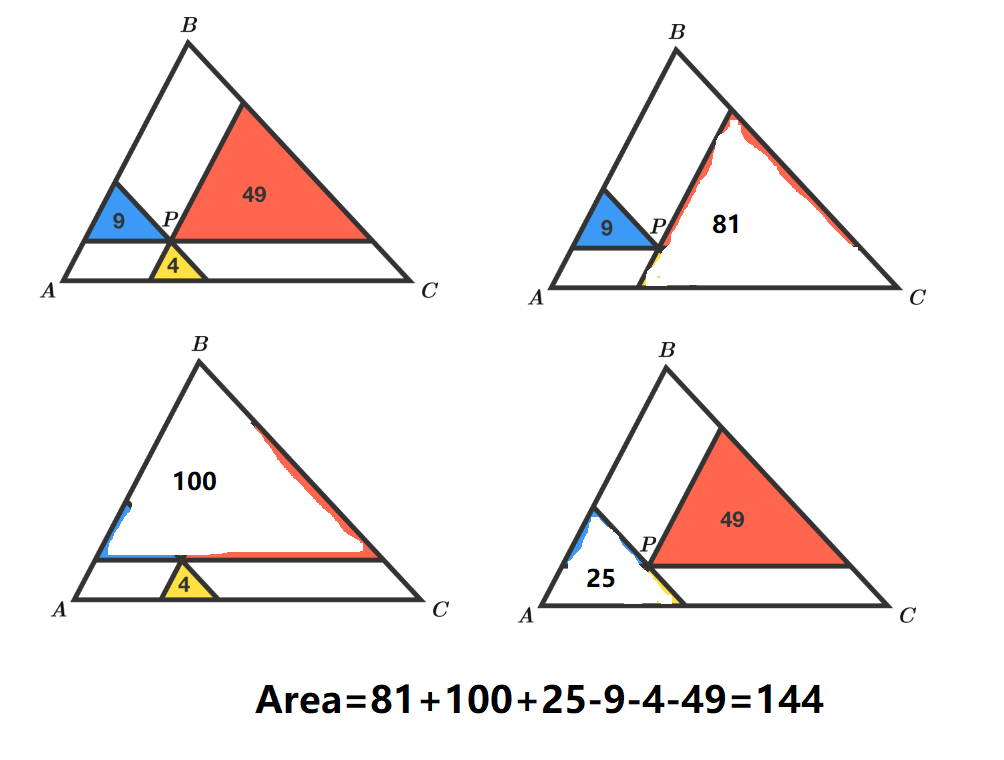
The three smaller triangles are similar to each other as well as to triangle A B C , as they were formed from lines parallel to its sides.
Then since the ratio of the areas of the three smaller triangles is 4 : 9 : 4 9 , the ratio of their respective sides must be 2 : 3 : 7 .
So if the base of the yellow triangle is 2 x , the bases of the blue and red triangles must be 3 x and 7 x respectively.
Then the base of triangle A B C is 1 2 x , so its base (as well its other sides) is 6 times as long as the base (and the other sides) of the yellow triangle.
Therefore the area of triangle A B C must be 6 2 = 3 6 times that of the yellow triangle, i.e. 3 6 × 4 = 1 4 4