Straight outta 2018

The Sylvester–Gallai theorem states that, given a finite number of points in the Euclidean plane, either all the points lie on a single line or there is a line which contains exactly two of the points. In our problem, since we restricted the latter case, all $2018$ points have to be aligned and so the minimum and only value for $m$ is $2018$ .

Some proofs can be found in the Wikipedia article.

All 2018 points must be in the line. Because even if one point is outside the lone, you get the opportunity of drawing a line through the point from any direction , and then you would have many lines passing through exactly two points, which would be a violation of the required conditon.

They must all be on the same plane so they must be on the same line or only have 2 connected points

Solution Using Extremal Principle* 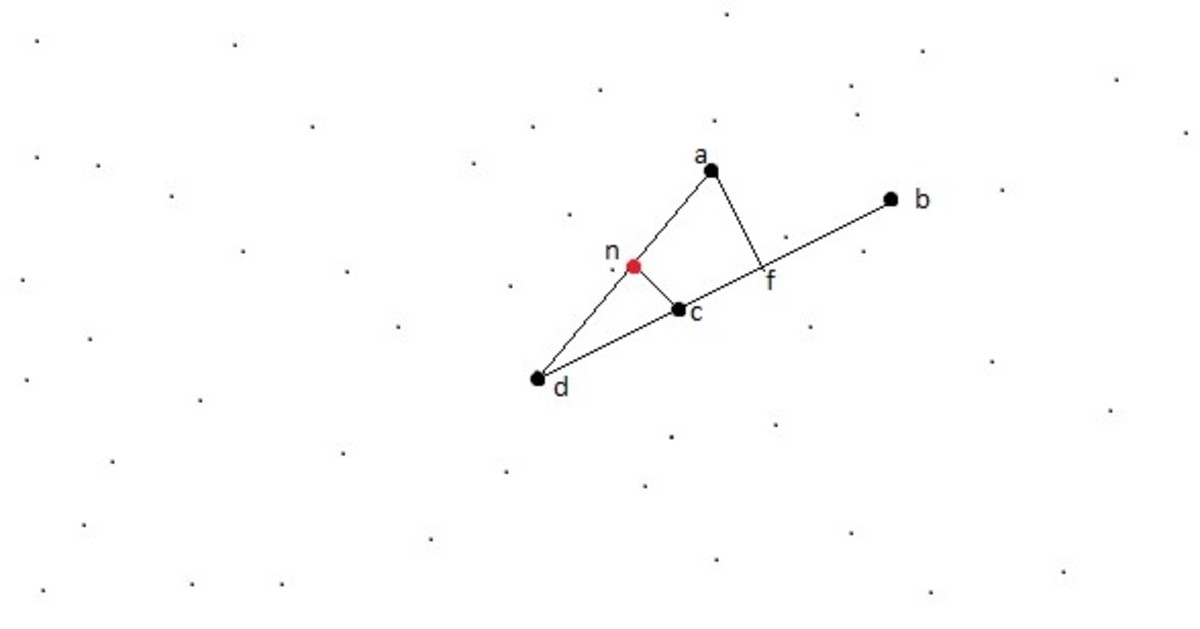Consider a line $l(bd)$ and a point $a$ such that of all pairs of distances between point and line the pair minimizes the distance between the point and the line; let $f$ be the foot of perpendicular from $a$ to the line. Assuming not all but more than 2 points on the line we have now at least 3 points on the line; two of which are on the same side of $f$ ; but now the length of perpendicular from $f$ to ad is yet shorter than length of $f$ ; Each time we make such an assumption we have a shorter length than the minimum allowed length. so we now allow the sequence of decreasing lengths to go on without any bounds nut that also cannot happen as a decreasing sequence of positive numbers(NOT INTEGERS) cannot be divergent; So by the two above observations we conclude that the sequence converges to 0 and indeed each term of the sequence is 0 (by the 1st lemma);

If any of the point is isolated then many lines can be drawn through the isolated point and the others(taken as 2nd point;assuming isolated point to be first) so we can't isolate any point out of the line. Hence the answer is 2018.

Start from smaller number, eg 3( because it's given) here all collinear

Now 4, notice that if you put the fourth point on the line passing from the previous three points then the condition is satisfied. But if you put the fourth point elsewhere then there are three lines passing from 2 points which we don't want, so now we can clearly see what's goin on.....

For any given number of points they must be all collinear for the given requirement

the questions states that the points are all on a plane. A plane is straight, and there are only 2018 points, thus the answer is 2018.