Straight(s) to the point
How many connecting lines are there between
3
7
points on the circle (cf. the exemplary figure below). Assume that the points do not overlap.
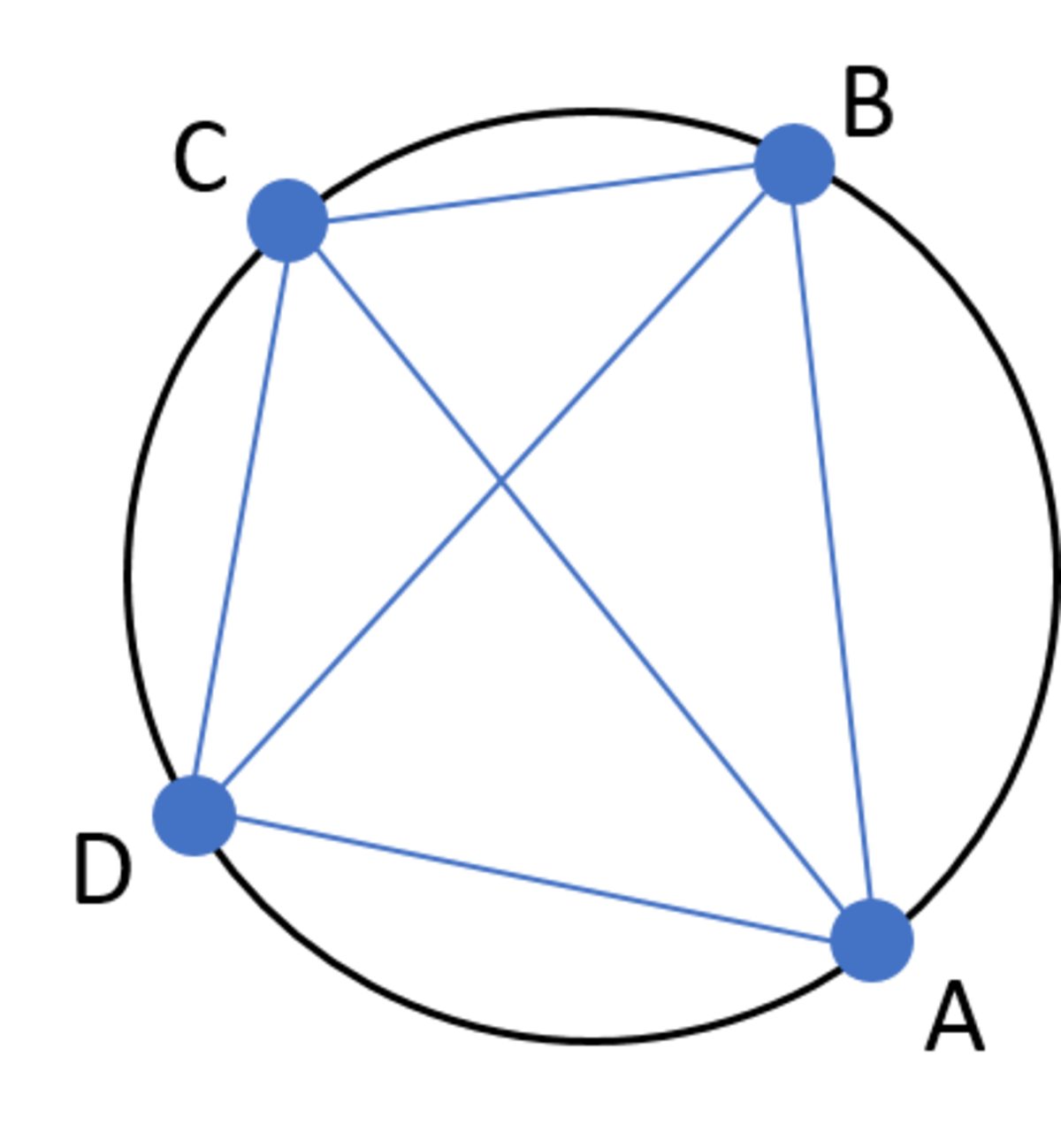 Example:
4
points can be connected with
6
segments.
Example:
4
points can be connected with
6
segments.
The answer is 666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Hey. I used other method
The difference of the no of points and the no of connecting lines is in an AP And hence I used V(n) - V(n-1) method
It is easy that way
The devil's number
Since every two points connect a segment, thus the number of segments is: ( 2 3 7 ) = 6 6 6
Nice thinking
See the sequence, if points = 4 then conecting lines = 3+2+1=6, and if points = 5 then conecting lines =4+3+2+1 =10. Conecting points = 37 then conecting lines =36+35+..............+2+1=666
Nice observation. Indeed the formula for the sum of the first n natural numbers is 2 n ( n + 1 ) . We can use it to rewrite my formula 2 n ( n − 1 ) = 2 n ( n + 1 ) − n , which is exactly what you did.
Log in to reply
Or else just view it directly as the sum of first n-1 natural numbers
The same sequence can also be observed in the 3rd diagonal column of Pascal's triangle.
A line is made by choosing 2 distinct points. Each of the 37 points on the circle can be connected with 36 other points, excluding itself. Thus the total number of line segment should be 3 7 × 3 6 . But no, we have double counted each line. Line A B is the same as line B A . Thus the answer will be divided by two ⟹ 2 3 7 × 3 6 = 6 6 6
Explicitly, the number of lines for n points is equal to 2 n × ( n − 1 ) which is actually ( 2 n )
Is my way of thinking right or wrong? Please see my solution! I want to know!
Number of diagonals in a polygon of n sides = 2 n ( n − 3 )
Number of sides= n
Number of total lines created
= n + ( 2 n ( n − 3 ) )
= 3 7 + 2 3 7 × 3 4 = 6 6 6
Go through permutation rule 37C2=666
There are 3 7 connected non-overlapping points.
We can consider it as a 3 7 − sided polygon.
Number of lines = Number of sides + Number of diagonals
Number of lines = 3 7 + 2 3 7 ( 3 4 ) (Thanks Google!)
Number of lines = 3 7 + 6 2 9 = 6 6 6
Yes, your way of thinking is correct but I would expect you to derive the formula for number of diagonals which is actually as easy as my derivation for the number of connecting points.
Log in to reply
Actually I don't know how it comes. That is why I wrote "Thanks Google"! :) Can you please tell me!?
I would encourage you to try to answer it by yourself. You can try to think in the way I solved the task (think what happens point by point). I am sure you can make it! :)
I copied some of your lines, sorry!
Let D ( n ) denote the number of diagonals in an n sided-polygon. n > 2
Firstly, we must show that the formula holds true for n = 3
D ( 3 ) = 2 3 ⋅ 0 = 0 ,which means no there is no diagonal in a triangle, which is true (base case is fullfiled).
Secondly, take arbitrary natural number k and assume:
D
(
k
)
=
2
k
(
k
−
3
)
Assuming this, we must prove that the formula is also true for
k
+
1
. Thus, we must show that
D
(
k
+
1
)
=
2
(
k
+
1
)
(
k
−
2
)
D
(
4
)
=
2
(
4
)
(
2
)
=
2
We know the number of diagonals in a quadrilateral is
2
.
So the induction step is also fullfiled. We have now fulfilled both conditions of the principle of mathematical induction. Therefore, by the principle of mathematical induction the formula is therefore true for every natural number n > 2 .
Is it right?
Log in to reply
Induction step
We know (from your diagram) thatD ( k + 1 ) = D ( k ) + ( k − 1 )
We need to show that it is equal to 2 ( k + 1 ) ( k − 2 ) .
D ( k + 1 ) = 2 ( k ) ( k − 3 ) + 2 2 k − 2
D ( k + 1 ) = 2 k 2 − 3 k + 2 k − 2
D ( k + 1 ) = 2 k 2 − k − 2
D ( k + 1 ) = 2 k 2 − 2 k + k − 2
D ( k + 1 ) = 2 k ( k − 2 ) + 1 ( k − 2 )
D ( k + 1 ) = 2 k + 1 ) ( k − 2 ) ,
which is indeed what we wanted, hence now I think it is fulfilled.
Do reply whenever you are free. I won't disturb you now! Sorry!
@Maria Paszkiewicz , please tell if it is correct or not!
@Vinayak Srivastava I saw your solution yesterday and I was planning to answer to you today in the evening (UTC+2) because I need to focus on my work during the day. Since you are so impatient and I got interrupted anyway, I am answering you now.
Actually, I was not expecting you to do the formal proof by mathematical induction but anyway I am very glad that you've tried. The problem with your proof is the induction step. You checked it only for k + 1 = 4 which is not general enough. How about 5 , 6 , … , n ?
Look once again at my drawing:
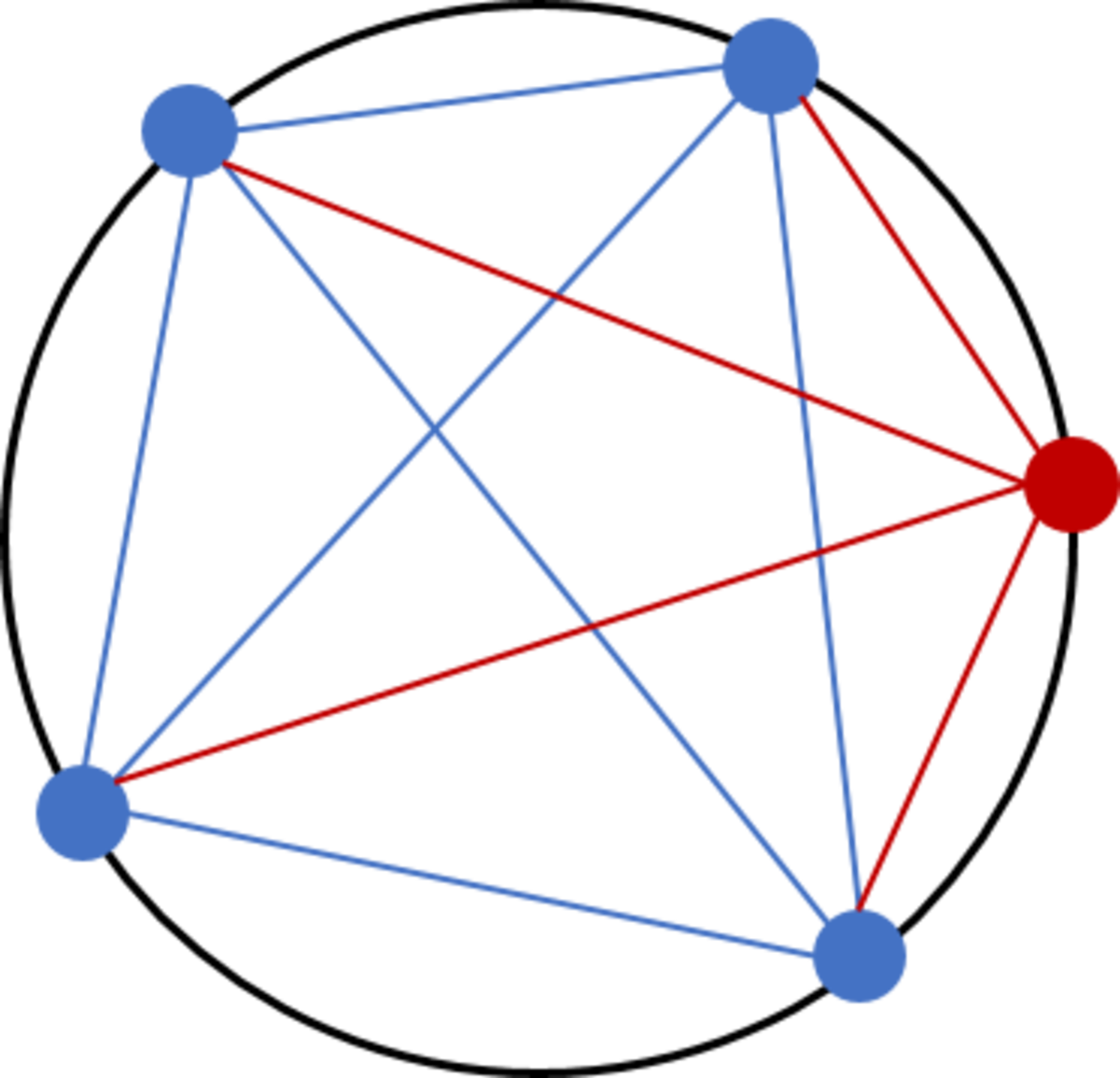 After the red point was added the number of diagonals increased by
3
. Why is that so? Because I can connect the red point with all others apart from the
2
neighbouring ones, so for
4
blue points it makes
2
additional diagonals. But at the same time one of the blue sides becomes a diagonal so the number of diagonals increases by
3
. (This part was tricky for me too) Coming back to the induction step, consider
k
points. Now, add a new point. How many diagonals can be drawn from the new point? The answer is:
k
−
1
diagonals. Now, in the place of your
D
(
4
)
you should write:
After the red point was added the number of diagonals increased by
3
. Why is that so? Because I can connect the red point with all others apart from the
2
neighbouring ones, so for
4
blue points it makes
2
additional diagonals. But at the same time one of the blue sides becomes a diagonal so the number of diagonals increases by
3
. (This part was tricky for me too) Coming back to the induction step, consider
k
points. Now, add a new point. How many diagonals can be drawn from the new point? The answer is:
k
−
1
diagonals. Now, in the place of your
D
(
4
)
you should write:
D ( k + 1 ) = D ( k ) + ( k − 1 ) .
Is this step clear? If yes, you can continue with it to show that D ( k + 1 ) = 2 ( k + 1 ) ( k − 2 ) and finish your proof.
Apart from the formal proof, try to make use of the first (short) part of my explanation to the task: "We can observe that every point can be connected with all the others...". You can think in the same way of the diagonals. From this consideration you should directly obtain the formula and say thanks to yourself and not to Google.
Log in to reply
Sorry for disturbing you, I did not know about that! I sincerely apologize!
Induction step
We know (from your diagram) thatD ( k + 1 ) = D ( k ) + ( k − 1 )
We need to show that it is equal to 2 ( k + 1 ) ( k − 2 ) .
D ( k + 1 ) = 2 ( k ) ( k − 3 ) + 2 2 k − 2
D ( k + 1 ) = 2 k 2 − 3 k + 2 k − 2
D ( k + 1 ) = 2 k 2 − k − 2
D ( k + 1 ) = 2 k 2 − 2 k + k − 2
D ( k + 1 ) = 2 k ( k − 2 ) + 1 ( k − 2 )
D ( k + 1 ) = 2 ( k + 1 ) ( k − 2 ) ,
which is indeed what we wanted, hence now I think it is fulfilled.
Do reply whenever you are free. I won't disturb you now! Sorry!
I did it myself and the answer is 666 Just add the number of points to the formula of the number of diagonals of a polygon
If there are n points, pick an arbitrary point A 1 and connect it with all other points which would form n − 1 segments(because 1 segment for each point except A 1 itself) then pick an adjacent point A 2 and connect it with all other points which would also be n − 1 segments but there is already a segment between A 2 and A 1 so to avoid overlap we subtract one so n − 2 segments. keep doing this till the last point and sum all the segments and you'll have ( n − 1 ) + ( n − 2 ) + ( n − 3 ) + ⋯ + 3 + 2 + 1 putting n = 3 7 gives 6 6 6
We can observe that every point can be connected with all the others. It would mean n ( n − 1 ) connections for n points. But in this way all the connections would overlap twice because we can go from point A to point B and from point B to point A (two directions but only one line). Therefore we must divide the previous result by 2 which gives
2 n ( n − 1 ) number of connecting lines.
For n = 3 7 we have 6 6 6 connecting lines.
Read further if you are interested in a formal proof.
I am going to show by mathematical induction that the formula is true for all natural numbers.
Let N ( n ) denote the number of segments between n points on the circle.
Firstly , we must show that the formula holds true for n = 1.
N ( 1 ) = 2 1 ⋅ 0 = 0 , which means no connecting line for one point what is true ( base case is fullfiled).
Secondly , take arbitrary natural number k and assume: N ( k ) = 2 k ( k − 1 ) . Assuming this, we must prove that the formula is also true for k + 1 . Thus, we must show that N ( k + 1 ) = 2 ( k + 1 ) k . Let’s see how the number of connections changes if we add one point. We can easily notice that we are just connecting the new
(
k
+
1
)
t
h
point with all the others.
It means we draw additional
k
segments so we end up with
N
(
k
)
+
k
connecting lines.
We must now check if
N
(
k
)
+
k
=
N
(
k
+
1
)
. Indeed
We can easily notice that we are just connecting the new
(
k
+
1
)
t
h
point with all the others.
It means we draw additional
k
segments so we end up with
N
(
k
)
+
k
connecting lines.
We must now check if
N
(
k
)
+
k
=
N
(
k
+
1
)
. Indeed
N ( k ) + k = 2 k ( k − 1 ) + k = 2 k ( k − 1 ) + 2 k = 2 k ( k + 1 ) = N ( k + 1 )
So the induction step is also fullfiled. We have now fulfilled both conditions of the principle of mathematical induction.
Therefore, by the principle of mathematical induction the formula is therefore true for every natural number.