Strange Delta-Wye Transform
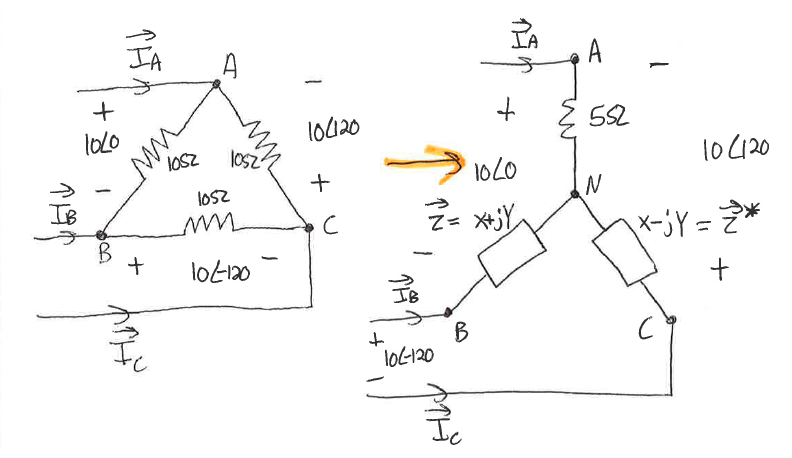
In power theory (notably three-phase AC power theory), the delta-wye transform can be used to convert a delta impedance network (left in diagram) into an equivalent wye network (right in diagram). The word "equivalent" here means that when supplied with identical node-to-node voltages ( V A B , V B C , V C A ), the network draws identical line currents ( I A , I B , I C ).
When doing these transforms, we are often converting a purely resistive delta network to a purely resistive wye network. Such wye networks are equivalent to their respective delta networks for all possible sets of boundary voltages.
However, we can derive a wye network consisting of inductive, capacitive, and resistive components which is equivalent to a purely resistive delta network for one particular set of boundary voltages.
Consider the purely resistive delta network on the left (with accompanying boundary voltages). Its properties are below:
Z A B = Z B C = Z C A = ( 1 0 + j 0 ) Ω V A B = 1 0 ∠ 0 ∘ V B C = 1 0 ∠ − 1 2 0 ∘ V C A = 1 0 ∠ 1 2 0 ∘
Suppose we transform the delta network into a (provisionally) equivalent wye network with the following properties:
Z A N = ( 5 + j 0 ) Ω Z B N = Z Z C N = Z ∗ V A B = 1 0 ∠ 0 ∘ V B C = 1 0 ∠ − 1 2 0 ∘ V C A = 1 0 ∠ 1 2 0 ∘
To 3 decimal places, what is the magnitude of Z , in ohms?
Details and Assumptions:
-
j
=
−
1
(the imaginary unit)
- The
∠
symbol denotes complex phase angle
- The
∗
superscript denotes
complex conjugation
The answer is 2.887.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Before we begin, we normalize all currents, voltages and elements by the values given below: voltages: 1 V , currents: 1 A ⇒ R , Z : 1 Ω The network equations remain the same in the process, but now all currents, voltages and elements represent their normalized dimensionless counterparts.
We use node analysis and loop analysis to directly get the equations for the delta- and wye-network, respectively. Alternatively, we could also use KCL and KVL, respectively, but it would take a bit longer: Δ : Y : I U : = ( I A I B ) = ( Y A B + Y A C − Y A B − Y A B Y A B + Y B C ) ( V A C V B C ) = 1 0 1 ( 2 − 1 − 1 2 ) ( V A C V B C ) = : Y Δ U = ( V A C V B C ) = ( Z A + Z ∗ Z ∗ Z ∗ Z + Z ∗ ) ( I A I B ) = ( 5 + Z ∗ Z ∗ Z ∗ Z + Z ∗ ) ( I A I B ) = : Z Y I The first equation holds for arbitrary voltages U , while the second equation holds for arbitrary currents I . By definition, if we choose the symmetric 3-phase voltages V A B = 1 0 , V C A = 1 0 w 3 = − V A C , V B C = 1 0 w 3 2 = 1 0 w 3 ∗ , ∣ ∣ ∣ ∣ ∣ w 3 : = e j 3 2 π = − 2 1 + j 2 3 both networks should be equivalent, i.e. both equations should hold at the same time! We insert the first into the second to eliminate I and notice we get an eigenvalue equation: U = Z Y I = Z Y Y Δ U = 1 0 1 ( 1 0 + Z ∗ Z ∗ − Z Z ∗ − 5 2 Z + Z ∗ ) U ∣ ∣ ∣ U is eigenvector of Z Y Y Δ with eigenvalue λ = 1 We could start calculating eigenvalues now, but it is easier to just expand the first row with matrix-multiplication: ( . . ) ∗ ⇒ V A C Z = − 1 0 w 3 = ( 1 0 + Z ∗ ) ( − w 3 ) + ( Z ∗ − 5 ) ( w 3 ∗ ) = − 5 ( 2 w 3 + w 3 ∗ ) + Z ∗ ( w 3 ∗ − w 3 ) = w 3 − w 3 ∗ 5 w 3 = j 3 5 w 3 , ∣ Z ∣ = 3 5 ∣ w 3 ∣ = 3 5 ≈ 2 . 8 8 7 Inserting Z into the second row, we verify our solution does indeed satisfy the entire eigenvalue equation. We notice Z is inductive, because its imaginary value is positive. Accordingly, Z ∗ is capacitive, because its imaginary value is negative.