Strange Equality Condition
Let x , y , and z be real numbers satisfying y + z x + z + x y + x + y z = 1 .
Find the maximum value of y + z x 2 + z + x y 2 + x + y z 2 .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Very clever!
Kay... what?
Amazing problem and solution!(+1)
k ( x , y , z ) = k ( x , y , z ) x + y + z ⟹ y + z x 2 + z + x y 2 + x + y z 2 ( 1 ( x , y , z ) ) = ( x + y + z ) ( y + z x + z + x y + x + y z ) = y + z x 2 + y + z x y + y + z x z + z + x x y + z + x y 2 + z + x y z + x + y x z + x + y y z + x + y z 2 = y + z x 2 + y + z x ( y + z ) + y + z x 2 + z + x y ( z + x ) + x + y z 2 + x + y z ( x + y ) = y + z x 2 + z + x y 2 + x + y z 2 + ( x + y + z ) = 0
Pretty neat problem
Can we know the value of x,y and z ?
Log in to reply
Take a look at this: https://brilliant.org/problems/simple-generalization-right/
@Dayan Wehbe Yes, there is a generalization. James Wilson has already showed you the link. Check out Rocco Dalto's solution.
Note that according to wolfram alfa, there are no real x, y, z satisfying the hypothesis...
Log in to reply
Did you set the partial derivatives to zero, and end up with ( y + z x ) 2 + ( x + z y ) 2 + ( x + y z ) 2 = 1 ? That was my mistake originally...
If there are no real x, y, z satisfying the problem, then the problem is flawed, and it cannot have an answer.
There are real x , y , z satisfying the original equation. Check out the solutions to this problem https://brilliant.org/problems/simple-generalization-right/
Note that if ( x , y , z ) is a solution to the equation y + z x + x + z y + x + y z = 1 , then for any r ∈ R , ( r x , r y , r z ) is also a solution. Let Q ( x , y , z ) = y + z x 2 + x + z y 2 + x + y z 2 be the quantity to maximise. Note that Q ( r x , r y , r z ) = r Q ( x , y , z ) . Hence there cannot be a maximum value unless Q ( x , y , z ) = 0 .
Do you have any references about this quality? I would like to know more about it. Any help is appreciated, thank you.
Log in to reply
I'm basically using the fact that the function is homogeneous (of degree 1) while the function which gives the condition is homogeneous of degree 0. Check the article "Homogeneous function" on wikipedia.
Let x + y + z = s Now ∑ c y c l i c y + z x 2 = ∑ c y c l i c s − x x 2 − s x + s x = ∑ c y c l i c ( s − x x ( x − s ) + y + z s x ) = − x − y − z + s = − s + s = 0
I have solustion!
x + y + z = ( x + y + z ) ( y + z x + x + z y + x + y z ) = y + z x 2 + x + z x y + x + y x z + y + z x y + x + z y 2 + x + y y z + y + z x z + x + z y z + x + y z 2 =
y + z x 2 + x + z y 2 + x + y z 2 + x + y z ( x + y ) + y + z x ( y + z ) + x + z y ( x + z ) =
y + z x 2 + x + z y 2 + x + y z 2 + x + y + z ⟹ y + z x 2 + x + z y 2 + x + y z 2 = 0
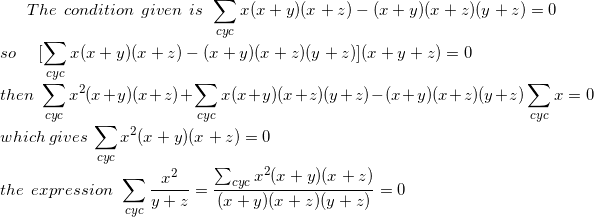
Note that x + y + z ⟹ y + z x 2 + z + x y 2 + x + y z 2 = ( x + y + z ) ( y + z x + z + x y + x + y z ) = y + z x ( x + y + z ) + z + x y ( y + z + x ) + x + y z ( z + x + y ) = y + z x 2 + y + z ( y + z ) x + z + x y 2 + z + x ( z + x ) y + x + y z 2 + x + y ( x + y ) z = y + z x 2 + z + x y 2 + x + y z 2 + ( x + y + z ) = 0
Therefore, the expression is always 0.