This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Discussions for this problem are now closed
Moderator note:
Great! One could generalize this to show that n ! − 1 = n ! ( n ! ) ! , where n = 2 , 3 , 4 , … .
But from 5040 * x! = 5040!, how did it become x! = 5039! ? Please explain?
Hi Diana
5 0 4 0 ! = 5 0 4 0 × 5 0 3 9 × ⋯ × 2 × 1
→ 5 0 4 0 × x ! = 5 0 4 0 × 5 0 3 9 × ⋯ × 2 × 1
Cancelling 5040 on both sides, we get
x ! = 5 0 3 9 × 5 0 3 8 × ⋯ × 2 × 1 , which is nothing but 5 0 3 9 !
It is pretty easy to generalize and see that x ! = x × ( x − 1 ) !
It's just n n ! , where n = 7 !
Obviously, n n ! = ( n − 1 ) ! , so 7 ! ( 7 ! ) ! = ( 7 ! − 1 ) ! = 5 0 3 9 !
x = 5 0 3 9
could you please explain how you did the second step!
x! = x * (x-1)!
7 ! = 5 0 4 0
( 7 ! ) ! = 5 0 4 0 !
x ! = 5 0 4 0 5 0 4 0 !
Canceling 5040 in the numerator and in the denominator, it remainders x ! = 5 0 3 9 !
x = 5 0 3 9
A one-liner: x ! = 7 ! ( 7 ! ) ! = 5 0 4 0 5 0 4 0 ! = 5 0 3 9 ! , so x = 5 0 3 9 .
same solution
Do you know of any solutions which don't require knowing/computing that 7! = 5040?
x! = (7!)! / 7! ; 7!= 5040 ; X! = 5040! / 5040 ; 5040!= 1(2 (3( 4 (5 ... (5039 (5040)))))))))...)))); 1(2 (3( 4 (5 ... (5039 (5040)))))))))...)))) / 5040 = 5039! ; X= 5039
value of 7!=5040 ; value of (7!)!=5040! ;
x!= (7!)!/7!
=(5040!)/5040
=(5040*5039*5038................*3*2*1)/5040
=5039*5038.............3*2*1
=5039!
Moderator note:
The expansion of 5 0 4 0 ! = 5 0 4 0 × 5 0 3 9 × 5 0 3 8 × ⋅ ⋅ ⋅ × 3 × 2 × 1 is not necessary. A simple recurrence relation n n ! = ( n − 1 ) ! should suffice.
Question:
x! = (5040!/5040).
Take for instance,
3!/3 = 6/3 = 2 =2!
In general,
n!/n = n-1!
Hence the answer is 5039!
X!= 7!x(7!-1)x(7!-2)x(7!-3)x(7!-4)....3x2x1 divided by 7!= (7!-1)! X!=(7!-1)! hence X = 7! - 1 = 5040-1 = 5039
7 ! ( 7 ! ) ! = 7 ! ( 7 ! ) ( 7 ! − 1 ) ! =(7!-1)!=5039!. So x=5039
x ! = 7 ! ( 7 ! ) ! = 7 ! 7 ! × ( 7 ! − 1 ) ! = ( 7 ! − 1 ) ! x = 7 ! − 1 = 5 0 4 0 − 1 = 5 0 3 9
x ! = 7 ! ( 7 ! ) ! 7 ! x ! = ( 7 ! ) ! 7 ! x ! = 7 ! ( 7 ! − 1 ) ! x ! = ( 7 ! − 1 ) ! x = 7 ! − 1 = 5 0 3 9
Here's a bit of fun: (7!)! is approximately 4 . 5 3 × 1 0 1 6 4 7 3
(7!)!=5040! , 7!=5040 -------------------------------- X!=5040(5039!)/5040 -------------------------------- X!=5039! ------------------------------------------------ X = 5039 ---------- proved
7 ! ( 7 ! ) ! = 7 ! 7 ! ⋅ ( 7 ! − 1 ) ! = ( 7 ! − 1 ) ! = > x ! = ( 7 ! − 1 ) ! = > x = 5 0 4 0 − 1 = 5 0 3 9
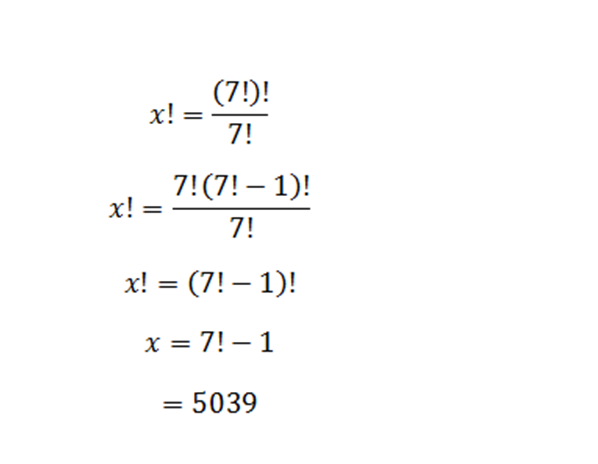
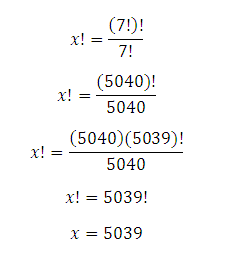
Relevant wiki: Factorials
x ! 5 0 4 0 ⋅ x ! x ! x = 7 ! ( 7 ! ) ! = 5 0 4 0 ! = 5 0 3 9 ! = 5 0 3 9