Strange Light Bulb Setup

In the first case the dissipation is $P=\frac{2 (120)^2}{R} \overline{\sin^2\omega_1 t}$ , where the time average is $\overline{\sin^2\omega_1 t}=1/2$ , so $P=120^2/R$ .

In the second case $P'=\frac{2 (120)^2}{R} \overline{(\sin \omega_1 t-\sin\omega_2 t)^2}$ . To calculate the average we use a trigonometric identity $(\sin \omega_1 t-\sin\omega_2 t)^2=\sin^2 \omega_1 t+\sin^2 \omega_2 t- 2 \sin \omega_1 t \sin \omega_2 t=\sin^2 \omega_1 t+\sin^2 \omega_2 t +\cos(\omega_1+\omega_2)t+\cos(\omega_1-\omega_2)t$ . The time averages are

$\overline{\sin^2 \omega_1 t}=1/2$ ,

$\overline{\sin^2 \omega_2 t}=1/2$ ,

$\overline{\cos (\omega_1+\omega_2) t}=0$ and

$\overline{\cos (\omega_1-\omega_2) t}=0$ .

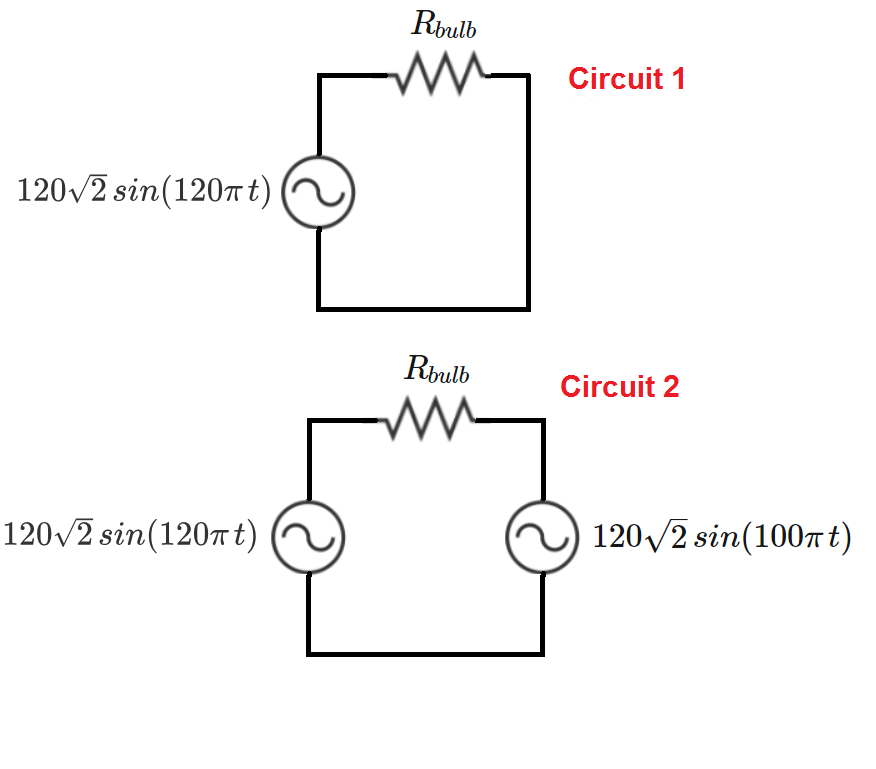
Therefore $P'=2P=80W$ . Please note that this argument works accurately if all of the oscillations involve an integer number of periods over the time of 1s. Easy to see that this is the case here. Also note that the the result is independent of the phase angle between the two oscillations, so if we use $\sin \omega_1 t+\sin\omega_2 t$ instead of $\sin \omega_1 t-\sin\omega_2 t$ , we get the same result. Finally, the power dissipation has a 10Hz oscillation between zero power and four times of the original power - the light bulb is in great danger of burning out. See the graph below.

Dissipated energy is the integral of power w.r.t. time over the given time interval. In the first case, power is (V^2)/R while in the second case it is ((V^2)+(v^2))/R, where V=120√2sin(120πt), v=120√2sin(100πt). Within the given limits, the value of the integral is (|V|^2)/2R, where |V| is the voltage amplitude. It is given that |V|=|v|=120√2. Also, it is given that (|V|^2)/2R=40. Therefore in the second case the dissipated energy is (2)(40)=80