Strange point in a strange polygon
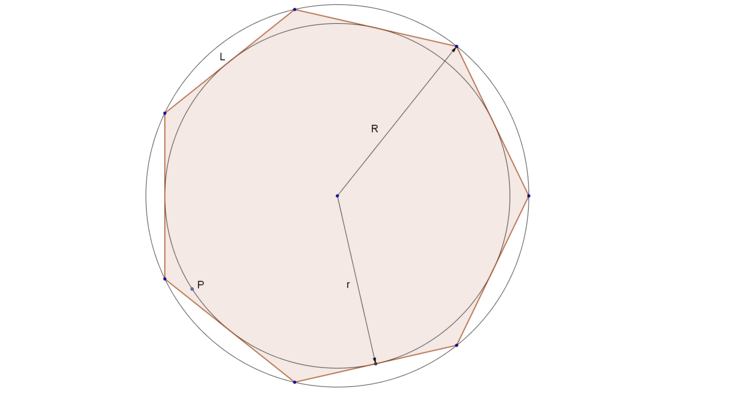 We have a regular polygon
A
with vertices
A
0
,
A
1
,
.
.
.
,
A
n
−
1
, and let
L
be its side. Now, let
P
be a point anywhere on the inscribed circumference of
A
.
We have a regular polygon
A
with vertices
A
0
,
A
1
,
.
.
.
,
A
n
−
1
, and let
L
be its side. Now, let
P
be a point anywhere on the inscribed circumference of
A
.
If we know that A 0 P 2 + A 1 P 2 + ⋯ + A n − 1 P 2 = ( 4 5 + 2 4 3 ) L 2 , find n , i.e., the number of sides of A .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I present a slightly more geometric method to obtain an expression for the L H S so that it's a factor of L 2 . The rest of the problem, finding n , follows from the other solutions.
Let B 0 , . . . , B n − 1 denote the point of tangency of the inscribed circumference. Since they are midpoints of each side of the polygon, namely A 0 A 1 , . . . , A n − 1 A 0 respectively. By the median formula we have A 0 P 2 + A 1 P 2 = 2 ( B 0 P 2 + 4 L 2 ) . Adding all the equations we obtain for each side L H S = ∑ i = 0 n − 1 ( B i P 2 + 4 L 2 ) . It is well known that ∑ i = 0 n − 1 B i P 2 = 2 n r 2 where r is the radius of the inscribed circle. We know 2 r L = tan ( n π ) , thus L H S = 2 n ( 4 tan 2 ( n π ) L 2 ) + n 4 L 2 = L 2 ( 2 tan 2 ( n π ) n + 4 n ) = 4 L 2 n ( sin 2 ( n π ) cos 2 ( n π ) + 1 )
r = 0 ∑ n − 1 A r P 2 = 2 sin 2 n π n L 2 = ( 4 5 + 2 4 3 ) L 2
2 sin 2 n π n L 2 = ( 4 5 + 2 4 3 ) L 2
Here, n can be large enough to have sin θ ≈ θ . ∴ sin 2 n π ≈ ( n π ) 2
∴ 2 sin 2 n π n L 2 = ( 4 5 + 2 4 3 ) L 2 ⇒ n 3 ≈ ( 9 0 + 4 8 3 ) π 2 ⇒ n ≈ 1 2
I obtained a different value for the summation, check that. But your approximation method is very good.
We can express all the vertices using complex numbers: A k = R e n 2 π k i , where R is the radius of the circumscribed circumference, but also the following condition holds using simple trigonometry: L = 2 R sin n π , so A k = 2 sin n π L × e n 2 π k i .
We can also express P in this way, where r is the radius of the inscribed circumference: P = r e θ i , but L = 2 r tan n π , so P = 2 tan n π L × e θ i .
Next, we calculate the required distances:
A k P 2 = ∣ A k − P ∣ 2
If we simplify that, we obtain A k P 2 = 4 L 2 × ( sin 2 n π 1 + cos 2 n π − sin n π tan n π 2 cos ( n 2 π k − θ ) )
Finally, let's take the sum:
k = 0 ∑ n − 1 A k P 2 = 4 L 2 × ( k = 0 ∑ n − 1 sin 2 n π 1 + cos 2 n π − 2 k = 0 ∑ n − 1 sin n π tan n π cos ( n 2 π k − θ ) )
The second sumation is 0 , using the formula for the summation of cosines in arithmetic progression. And we are left with:
k = 0 ∑ n − 1 A k P 2 = 4 L 2 n × sin 2 n π 1 + cos 2 n π
So, we have to solve 4 L 2 n × sin 2 n π 1 + cos 2 n π = ( 4 5 + 2 4 3 ) L 2 ⟹ n ( 1 + cos 2 n π ) = ( 1 8 0 + 9 6 3 ) sin 2 n π
We can use trial and error method to obtain that n = 1 2 or plot the equation for n ≥ 3 . If you know a better method to solve that, I'd like to know.