Strange region
What is the area of the region defined by the following set of inequalities?
( 1 ) ( 2 ) 0 < 2 x y < 1 0 < 2 x + y < 1
If the area is A , give ⌊ 1 0 0 A ⌋ .
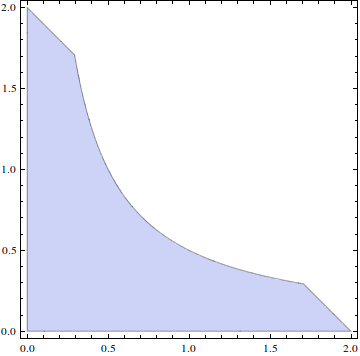
The answer is 146.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I converted the two inequalities into equations:
- y = 2 x 1
- y = − x + 2
Found the x-value of the intersections:
− x + 2 = 2 x 1
− 2 x 2 + 4 x − 1 = 0
x = 1 ± 2 2
And summed the three integrals:
∫ 0 1 − 2 2 ( − x + 2 ) + ∫ 1 − 2 2 1 + 2 2 ( 2 x 1 ) + ∫ 1 + 2 2 2 ( − x + 2 ) = 1 . 4 6
I kind of winged it the whole way because I have no idea how to deal with inequalities.
Log in to reply
exactly the way I did :)
That's a perfectly valid way of doing it, as long as you're sure that the bounds of your integrals correspond to the region given.
+1 for your nice way of explaining the second method!
That's kind of coordinate transformation, isn't it? I think it's complicated, I just used 'classical' approach to solve this problem, but +1 for your solution.
Log in to reply
Yes, it is a coordinate transformation! It can be a very useful tactic in solving more complex problems. I just wanted to introduce it to the solvers of this problem.
A = 2 − ∫ 1 − 2 1 1 + 2 1 ( 2 − x ) − 2 x 1 d x = 1 . 4 6 7 . . .
So, ⌊ 1 0 0 A ⌋ = 1 4 6
Suggestion to Michael: For Calculus problems such as these, where the wording is very clear, it acts against the difficulty of your problem if you give the graph. This should be left for the solver to do, as that is part of the problem.
My Solution : So, given the diagram, we want to find the area of the first part, governed by the line, and the second part, governed by the curve, and the third part, re-governed by the line. For this, we need the two intersection points of the graphs of x y = 2 1 and x + y = 2 .
We get that the x -coordinates for the two intersection points are 1 − 2 2 and 1 + 2 2 . Thus, the area is
A = ∫ 0 1 − 2 2 ( 2 − x ) d x + ∫ 1 + 2 2 2 ( 2 − x ) d x + ∫ 1 − 2 2 1 + 2 2 ( 2 x 1 ) d x .
Evaluating this is the easy part. Multiplying this by 1 0 0 and taking the floor, we get 1 4 6 .
The intersection points of the line and the hyperbolic region are given by, ((1-1/sqrt(2)) , (1+1/sqrt(2))) and ((1+1/sqrt(2)) , (1-1/sqrt(2)))
The given area A is simply divided into the following three parts:
-
Integral of (-x+2) from 0 to (1-1/sqrt(2))
-
Integral of (1/(2x)) from (1-1/sqrt(2)) to (1+1/sqrt(2))
-
Integral of (-x+2) from (1+1/sqrt(2)) to 2
Calculating the areas under the three regions and adding will give us the total area A bounded between the given inequalities...
We can find the area by taking the area between the curves y = − x + 2 and y = 2 x 1 and then subtracting that from 2 1 ( 2 ) ( 2 ) = 2 . Clearly the former function is on top. We need to also find their points of intersection.
− x + 2 = 2 x 1 → 2 x 2 − 4 x + 1 = 0 → 2 ( x − 1 ) 2 = 1
\((x-1)^2 = \frac{1}{2}
\(x - 1 = \pm \frac{1}{\sqrt{2}}\)
x = 1 ± 2 1
So now we know our limits of integration. Now, we can integrate.
∫ − x + 2 − 2 x 1 d x
[ 2 − x 2 + 2 x − 2 1 ln x ] 1 − 2 1 1 + 2 1
Using a calculator to find this value, we get a final answer of 1 4 6 .
For an exact form:
2 − 1 ( ( 1 + 2 1 ) 2 − ( 1 − 2 1 ) 2 ) + 2 ( 1 + 2 1 − ( 1 − 2 1 ) − 2 1 ( ln ( 1 + 2 1 ) − ln ( 1 − 2 1 )
Using factorizations ( a + b ) 2 = ( a + b ) ( a − b ) , this is
2 − 1 ( ( 2 ) ( 2 ) + 2 ( 2 ) − 2 1 ln 2 1 ( 1 + 2 1 ) 2
2 − 2 1 ln ( 3 + 2 )
So the area is 2 − 2 + ln ( 3 + 2 ) 2 .
Also sorry brilliant!I have failed you
Check to see that mathematical symbols load properly
:(
There are two good ways to solve this problem. The first is to note that the region can be broken up into three parts, one of which is defined by { 0 < x < 2 − y ∣ 0 < y ≤ 1 − 2 1 } , the second of which is { 0 < x < 2 y 1 ∣ 1 − 2 1 < y < 1 + 2 1 } , and the third of which is { 0 < x < 2 − y ∣ 1 + 2 1 ≤ y < 2 } . We then perform three double integrals ∬ dA with these limits to obtain an answer of A = − 2 + 2 + 2 1 lo g ( 3 + 2 2 ) ≈ 1 . 4 6 7 ⇒ ⌊ 1 0 0 A ⌋ = 1 4 6 .
However, I'd like to introduce a different manner of calculating the area that could be more useful in another context where the region provided cannot be so easily broken up. The differential form dA is expandable to dx ∧ dy , the wedge product of differentials dx and dy . Define u and v such that u = 2 x y and v = 2 x + y . Then, solve for x and y to get x = v ± v 2 − u / 2 and y = v ∓ v 2 − u / 2 . For each solution x and y , the region defined by 0 < u < 1 and 0 < v < 1 is half of the problem region, as the two regions are symmetric over the line y = x . Take the first solution x and y . We find that dx = 4 v 2 − u / 2 1 du + ( 1 + v 2 − u / 2 v ) dv and dy = − 4 v 2 − u / 2 1 du + ( 1 + v 2 − u / 2 v ) dv . Then, dx ∧ dy = ( 4 v 2 − u / 2 1 du + ( 1 + v 2 − u / 2 v ) dv ) ∧ ( − 4 v 2 − u / 2 1 du + ( 1 + v 2 − u / 2 v ) dv ) . Note that the wedge product is distributive and anticommutative, and that du ∧ du = dv ∧ dv = 0 . So, dx ∧ dy = ( 4 v 2 − u / 2 1 ) ( 1 + v 2 − u / 2 v ) du ∧ dv + ( 1 + v 2 − u / 2 v ) ( − 4 v 2 − u / 2 1 ) dv ∧ du = ( 4 v 2 − u / 2 1 ) ( 1 + v 2 − u / 2 v ) du ∧ dv − ( 1 + v 2 − u / 2 v ) ( − 4 v 2 − u / 2 1 ) du ∧ dv = 2 v 2 − u / 2 1 du ∧ dv .
So, ∬ dA = ∬ dx ∧ dy = ∬ 2 v 2 − u / 2 1 du ∧ dv .
We then perform the integral ∫ 0 1 ∫ 0 1 2 v 2 − u / 2 1 du dv and multiply by 2 (because, remember, this is one of two symmetric regions) to get the same answer as before, A = − 2 + 2 + 2 1 lo g ( 3 + 2 2 ) ≈ 1 . 4 6 7 ⇒ ⌊ 1 0 0 A ⌋ = 1 4 6 .