Strange solid
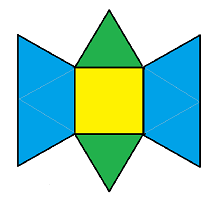
Consider the figure above, which is made up of
- two green equilateral triangles with side length 1
- one yellow unit square
- two blue trapezoids (each made up of three equilateral triangles with side length 1).
The shape is then folded along the sides of the square so that the sides of the triangles and trapezoids can be glued together. What is the volume of the final three-dimensional object?
Give your answer to 2 decimal places.
The answer is 0.47.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It can be also thought of as half of a unit octahedron and two unit tetrahedrons.
The shape can be seen as a square pyramid with two tetrahedra attached. Its volume is therefore half the volume of a regular octahedron of side 1 plus twice the volume of a regular tetrahedron of side 1 , namely 3 2 .
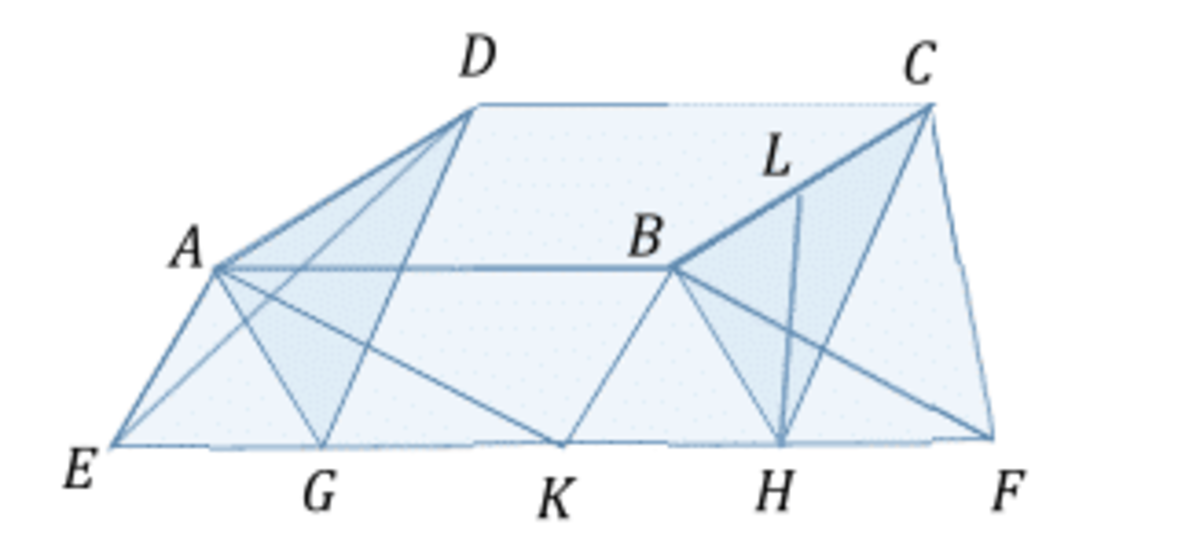 Top of the object is a square ABCD, side 1. The ends are equilateral triangles ADE and BCF, also side 1. The trapezoids are ABFE and DCFE.
Top of the object is a square ABCD, side 1. The ends are equilateral triangles ADE and BCF, also side 1. The trapezoids are ABFE and DCFE.
The solid can be sliced by two planes, both perpendicular to line EF, one a plane of triangle ADG, the other triangle BCH. The operation results in three solids: a triangular prism in the center and two triangular pyramids on the ends. Triangles ADG and BCH are congruent and one or the other of them functions as the base of every one of these solids.
Value of BH can be calculated from equilateral triangle BFK with sides 1. B H = 2 3 . Also C H = B H = 2 3 from symmetry or by equivalent calculation.
So the triangle BCH has sides 1 , 2 3 , and 2 3 . Height HL of the triangle is from Pythagorean theorem 2 1 . This gives us the area of the base as A = 2 2 1 .
Volume of the prism is V p = 1 × A = 2 2 1 .
Volume of the end piece is V e = 3 1 × 2 1 × A = 6 2 1 .
Putting it all together V = V p + 2 V e = 2 2 1 + 3 2 1 = 3 2 .
Nice... Did you just fold that up today? 😃
Log in to reply
Yes :) . It helped me to solve the question easily.
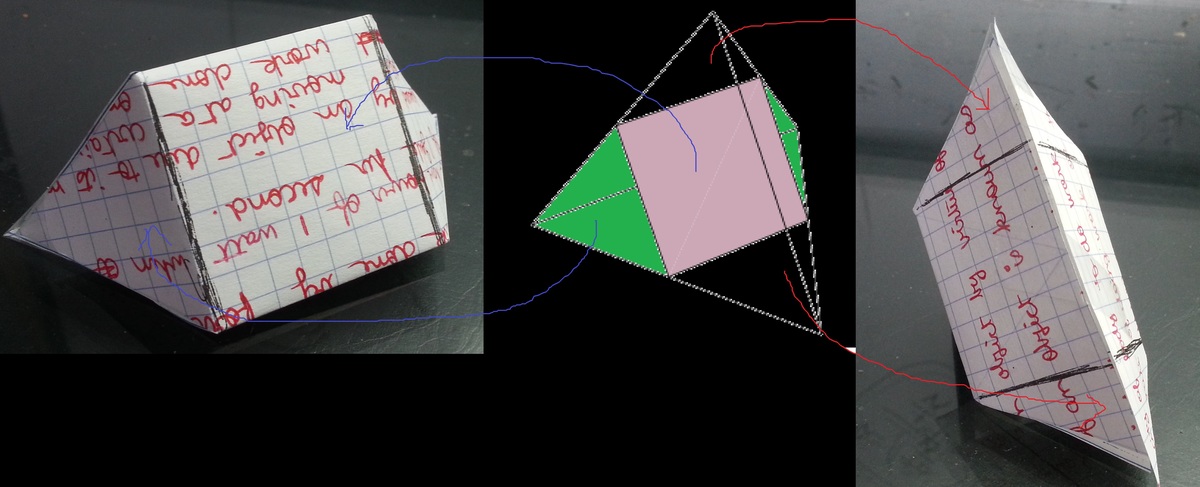
The final 3D object is actually half of a regular tetrahedron (with edge length two) cut parallel to, and half way between, two opposite edges.
The volume of a regular tetrahedron is given by:
V t e t r a h e d r o n = 6 2 a 3 ≈ 0 . 9 4
where a is the edge length, which is 2 in this case.
So, the volume of our solid will be:
V ≈ 2 0 . 9 4 = 0 . 4 7