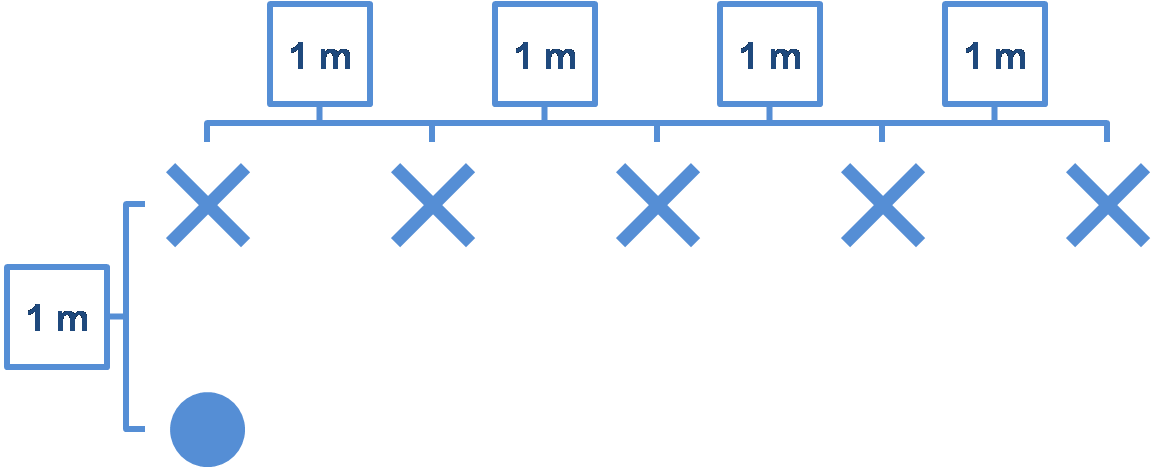
Streetlamps in a line

Let us label each streetlamp Lamp A to E from west to east. You receive $x$ light from Lamp A, and through the Pythagorean theorem and the inverse square law, you find that you receive $\frac{x}{1+1^{2}}=\frac{x}{2}$ light from Lamp B, $\frac{x}{1+2^{2}}=\frac{x}{5}$ light from Lamp C, $\frac{x}{1+3^{2}}=\frac{x}{10}$ light from Lamp D, and $\frac{x}{1+4^{2}}=\frac{x}{17}$ light from Lamp E. Thus, you receive $\frac{158x}{85}$ light from the entire line of lamps. Knowing that you receive $x$ light from Lamp A (the westernmost streetlamp), all that remains is to divide the last two values to obtain a value of $\frac{158}{85}$ , or, to 3 decimal places, $\boxed{1.859}$ .