Stretch and Accelerate!

Classical Mechanics Level 2

A block of mass $m$ and another block of mass $M$ are attached together with a spring of spring constant $k$ and are at rest on a smooth frictionless floor. A constant force $F$ is applied to the block of mass $M$ to accelerate the system. What will be the maximum elongation (length) of the spring during the time in which the force is applied?

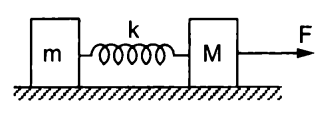
Assumptions and Details:

Force applied on $M$ is perfectly horizontal.
Let there be a coordinate system $K'$ that is positive to the right and negative to the left along with your reference frame.
Represent the expression in terms of $m$ , $M$ , $k$ , and $F$ .

\frac{2Fk}{m + M}

\frac{k(m + M}{2mF}

\frac{m + M}{2Fk}

\frac{2mF}{k(m + M)}

\frac{mx1 + Mx2}{m + M}

1 solution

Raghu Alluri
Mar 23, 2019

Since there is a force acting on this system we must take into account that the center of mass of the system will also be accelerating at the same rate as the two blocks and also that the momentum is not conserved with respect to any inertial frame. In any case this problem can still be solved with respect to an inertial frame, however, it would most likely end up needing to know the instantaneous velocity of that object at some certain time. So instead we can solve it another way.

Let's take a reference frame, A, moving at the acceleration of the center of mass $a_{cm}$ .

$a_{cm} = F / (m + M)$

So with respect to the reference frame A, we can conclude that there must be inertial forces (fictitious forces) acting on both of the objects of the system. So on the block with mass $m$ there would be an inertial force of $ma_{cm}$ and for the block of mass $M$ , there would be an inertial force of $Ma_{cm}$ . Now we can write the net forces acting on both blocks which are external.

$F_1 = ma_{cm} = mF / (m + M)$

$F_2 = F - Ma_{cm} = F - MF / (m + M)$

We can also imagine some arbitrary displacements of the blocks with respect to the reference frame. So, for example, we can say that the $m$ has moved $x_a$ to the left and that $M$ has moved $x_b$ to the right. This displacement is temporary and the blocks come to rest when the force of the spring is equal to the magnitude of the fictitious force. This would then mean that the length of the spring $x_o$ would be the sum of them, $x_b + x_a$ .

Also, we should note that since the system is stationary to the frame A, there is no change in kinetic energy over time. Instead, there is only change in spring potential energy. We can express this change in terms of work done on the system,

$W_{net} = ΔU_s = k(x_b + x_a)^2 / 2$

$W_{net} = W_{F_1} + W_{F_2}$

Since all forces are constant,

$W_{net} = mFx_b / (m + M) + mFx_a / (m + M) = mF(x_b + x_a) / (m + M)$

Thus we get the following equation with respect to the accelerating frame A,

$k(x_b + x_a)^2 / 2 = mF(x_b + x_a) / (m + M)$

Rearranging this equation we get the expression below. Thus we can conclude that the maximum elongation of the spring will be,

$x_o = 2mF / k(m + M)$

Stretch and Accelerate!

1 solution

0 pending reports