String and Pillar
A string of length L o is tied to a circle of radius R and a very tiny ball. The ball is given an initial angular velocity ω o perpendicular to the string. The string is initially perpendicular to the radius from the center of the circle to the point where the string is tied to it. The string wraps around the circle and there is no friction or gravity. How long does it take, in seconds, for the ball to touch the circle. Input your answer to the nearest hundredth.
Details and Assumptions:
- The string (red in picture) has effectively 0 width and 0 mass.
- The values of R and L o are such that that ball hits the circle.
- The circle (black) doesn't move and has radius R = 2 1 L o .
- The ball (blue) has a negligible radius but still has mass.
- ω o = 0.25 rad/s
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
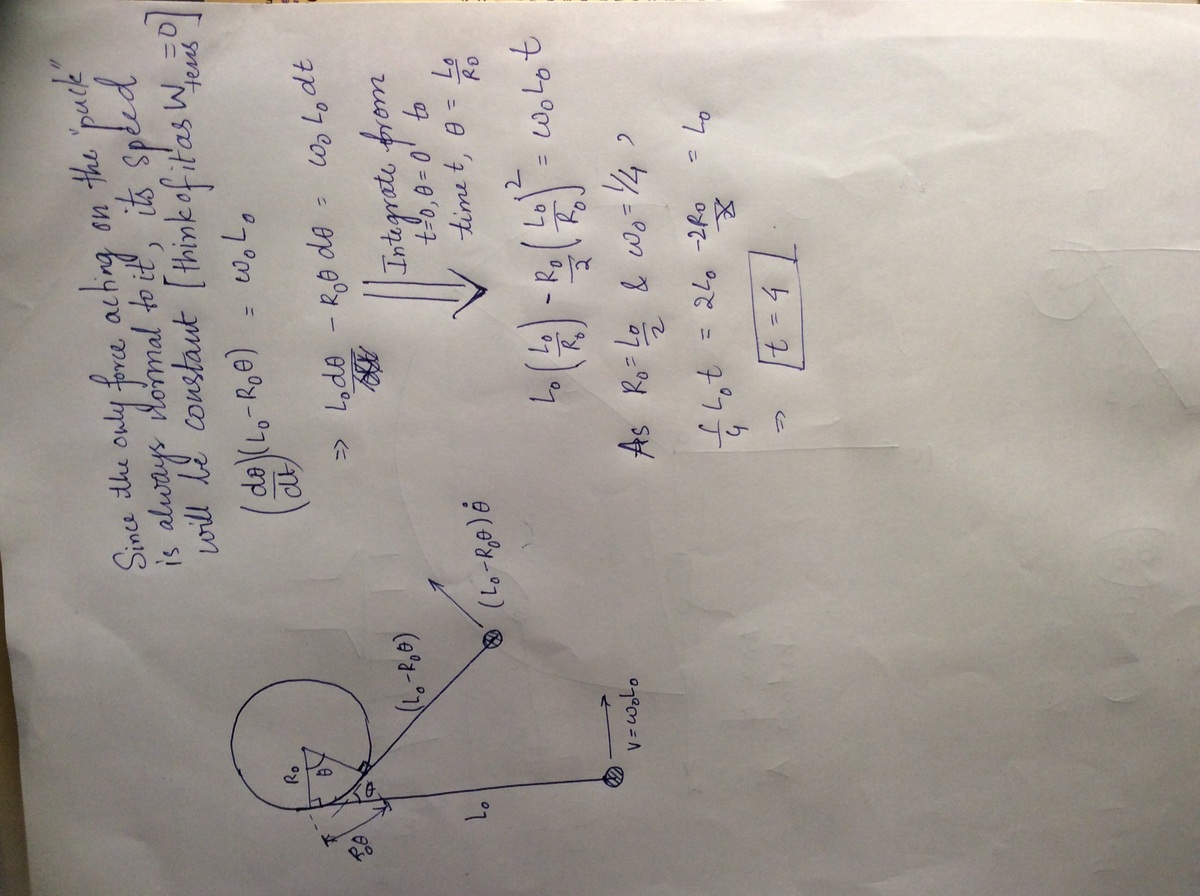
Nice solution!
There is no friction and gravity in the system. Throughout the process of the 0-mass string wrapping around the circle, energy is conserved and the only energy involved is kinetic of energy of the tiny ball. Let the mass of the ball be m , its initial velocity be v 0 and instantaneous velocity at time t be v . Then, we have 2 1 m v 2 = 2 1 m v 0 2 ⟹ v = v 0 ⟹ L ω = L 0 ω 0 , where L and ω and the instantaneous length and angular velocity of the loose string respectively.
Let the angle wrapped by the string around the circle at time t be θ . Then, we have:
L ω ( L 0 − θ R ) ω ( L 0 − 2 θ L 0 ) ω ( 1 − 2 θ ) ω ( 1 − 2 θ ) d t d θ ∫ ( 1 − 2 θ ) d θ θ − 4 θ 2 + C 0 − 0 + C ⟹ θ − 4 θ 2 2 − 4 2 2 ⟹ t = L 0 ω 0 = L 0 ω 0 = L 0 ω 0 = ω 0 = ω 0 = ∫ ω 0 d t = ω 0 t = 0 = ω 0 t = 0 . 2 5 t = 4 s where C is the constant of integration. When t = 0 , θ = 0 When the string is all wrapped up, L 0 = 2 θ L 0 ⟹ θ = 2
Sir, if theta is defined as the angle wrapped by the string, it is important to justify why dtheta over dt is the angular velocity of the puck. For that, some little geometry is needed (this is one more place where we use the fact that the pillar is cylindrical !)
@Trevor Arashiro Wow!!! This is where I feel bad abt making an easy question hard.......I actually found out the parametric equation of the Involute of the circle.....then, integrated it to find the arc length.......and then used time=distance/speed.........!!!! I actually converted this into calculus!!! XD!!! Still....a great Problem!!!