String of Squares
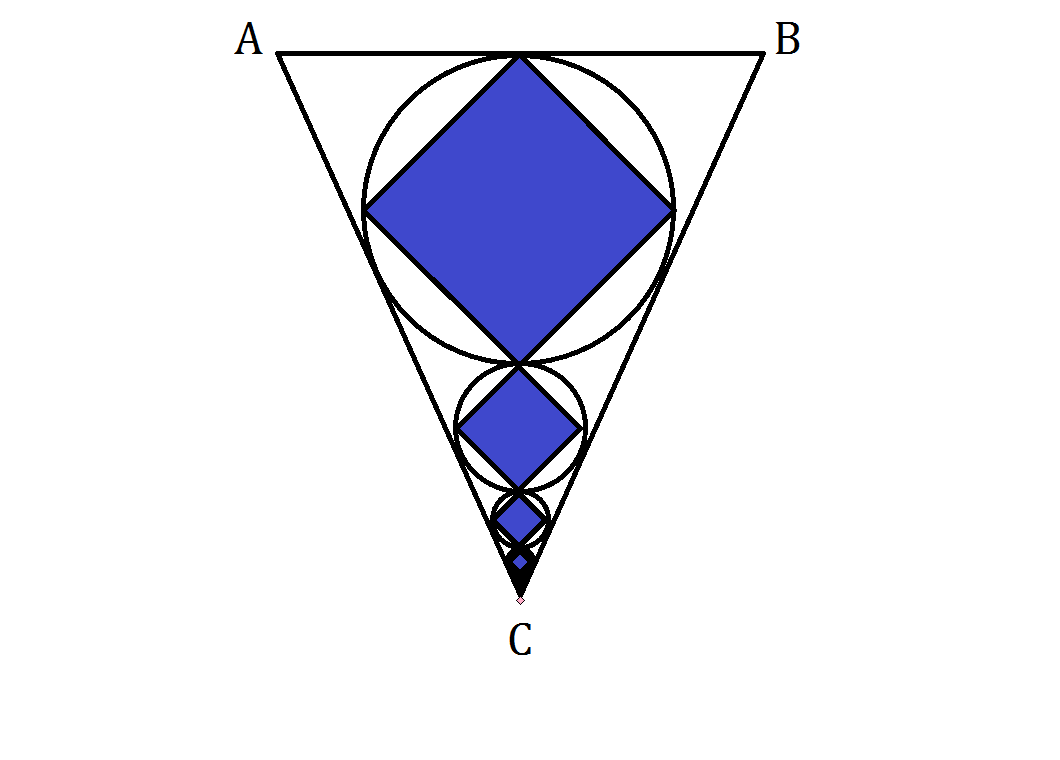
A big mobile is outlined from an isosceles triangle , where . and .
First, the inscribed circles are drawn recursively touching one another endlessly towards to the vertex before the blue squares are inscribed in those circles along the height from vertex to the base. Finally, a pink square of is attached to the vertex outside the triangle for decoration.
What is the total area of all colored squares (in ).
The answer is 2017.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By Pythagorean theorem, the height from vertex C to base A B = 1 2 5 2 − 3 5 2 = 1 2 0
A radius of an inscribed circle inside a triangle = perimeter 2 × Area of triangle = 7 0 + 1 2 5 + 1 2 5 7 0 × 1 2 0 = 3 2 0 8 4 0 0 = 4 1 0 5 .
Therefore, the biggest incircle's diameter = 2 1 0 5 = 5 2 . 5
Then for the next second incircle, the new height will be 1 2 0 − 5 2 . 5 = 6 7 . 5 . Thus, the ratio of the similar smaller triangle to the original one = 1 2 0 6 7 . 5 = 1 6 9 .
Because of similarity, the ratio for the next recursive incircle will always be 1 6 9 , and so it is a geometric series for the blue squares with each square's area = 2 d 2 where d is the diameter of the incircle or the diagonal of the square. It should be noted that the ratio of the next recursive square is ( 1 6 9 ) 2 as two sides are multiplied.
Thus, the total blue squares' area = 2 1 ( 1 − ( 1 6 9 ) 2 5 2 . 5 2 ) = 2 5 2 . 5 2 × 1 7 5 2 5 6 = 2 0 1 6 .
Now don't forget the little last pink unit square. The total colored area will then equal 2 0 1 6 + 1 = 2 0 1 7 .