String Swing
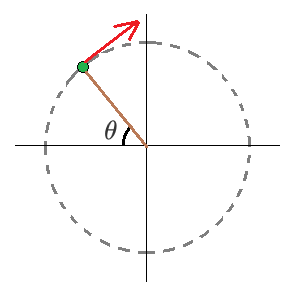
A string of length L swings clockwise in a circle in the x y plane, with one end fixed at the origin. A ball is attached to the other end of the string as shown below. The ball maintains a constant speed v 0 as it swings.
When the string is at an angle θ with respect to the negative x axis (see graphic), the ball detaches from the string and flies through the air on a standard kinematic trajectory. The ball eventually lands on the positive x axis at position x f .
Which value of θ (in degrees) maximizes x f ?
Details and Assumptions:
- Gravity
g
=
1
0
m/s
2
in the negative
y
direction
-
L
=
1
m
-
v
0
=
5
m/s
The answer is 62.9172.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for the solution. I also solved numerically
Thank you for posting the problem! It is an original case for testing conventional knowledge in physics, with the added challenge of finding the right value.
Log in to reply
@Gabriel Chacón Sir. Your solution is awesome. I understand very quickly. Sir please can you suggest me good problems book in physics???
Indeed, as the initial speed approaches infinity, the result coincides with conventional wisdom
I missed the − L cos θ .
Log in to reply
I too bro, didn't notice that x f was on positive x axis.
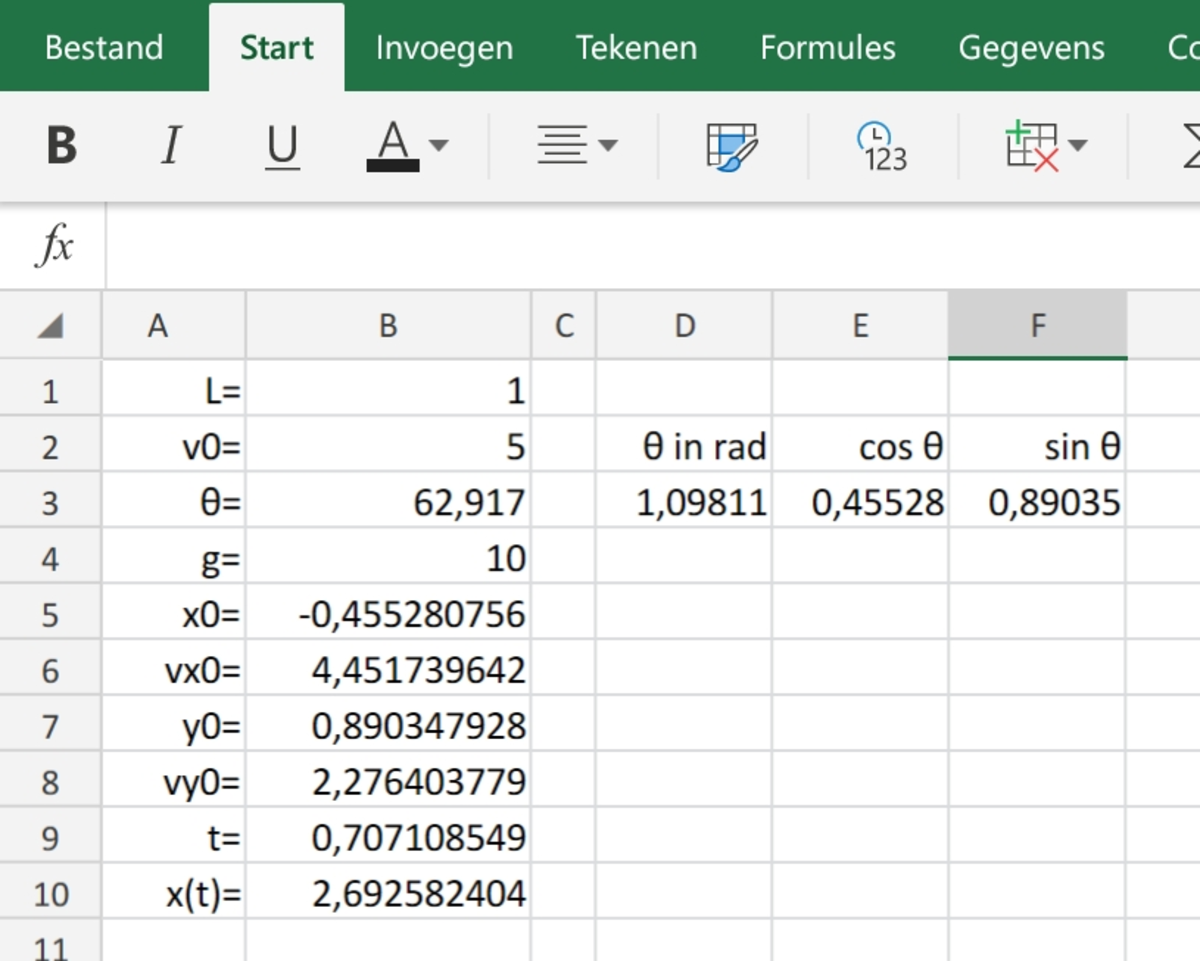
First tried analytically, found an expression for x(θ) but setting its derivative to 0 got too messy (see pic below).
Then used Excel entering the formulas:
x 0 = − L cos θ
y 0 = L sin θ
v x 0 = v 0 sin θ
v y 0 = v 0 cos θ
t = ( v y 0 + v y 0 2 + 2 g y 0 ) / g
x ( t ) = x 0 + v x 0 t
and tried values for θ.
θ
=
6
2
.
9
1
7
gave the largest value for x.

The ball will follow the equations of projectile motion:
x y = = − L cos θ + v 0 sin θ t L sin θ + v 0 cos θ t − 2 1 g t 2
We solve for t when y = 0 :
t + = g v 0 cos θ + v 0 2 cos 2 θ + 2 g L sin θ
We plug this result for the value of t in the first equation to get the x-coordinate:
x = − L cos θ + v 0 sin θ g v 0 cos θ + v 0 2 cos 2 θ + 2 g L sin θ
To maximize x ( θ ) we should solve d θ d x = 0 , which at first looks like it requires numerical treatment. So I decided to find the maximum using Geogebra (indulgence, please!). This is the plot and the numerical result I got: