String Tensions

Formulas aren't actually necessary to figure out the answer.

The strain on the vertical string is the same throughout the entire string, while the strain on the horizontal string will be focused around a single point. Since the tension on that point will be greater than any other point on the vertical string, and either string will break when a point on that string gets to a certain tension, the horizontal string will reach that certain tension first and break.

draw a free body diagram. the horrizontal string will sag a bit but the force vector takes the weight that is W=2×F×sin(1°) so F force in string would need to be high in order take weight W with a low angle like 1 degree

It seems to depend on how stretchy the strings are. Tension in vertical string is mg Each side of horizontal string has vertical component mg/2 = T sin(a) where a is the angle the string dips by and T is the tension. This allows T in the horizontal string to be less than mg for angles exceeding 30 degrees. This will happen if the strings stretch by more than a factor of 2/sqrt(3) before breaking.

The answer depends on the angles between the strings at the junction, which in turn depend on how much slack the upper (it's never truly horizontal) string has initially and how much it stretches under tension.

When the upper string is almost straight, as in the illustration, it has a very high tension and breaks first.

If the strings form three angles of 120 degrees each, the strings have the same tension and break at the same time. If the upper string gets even longer (if it hangs very low, it can effectively almost double itself), then the lower string has more tension and breaks first.

Does anyone find it odd that the tension in the string increases to infinity at the slightest onset of loading? Without accounting for the elasticity of the string the mechanics don't strictly forbid you from independently varying the angle theta in such a way that a mere feather weight loading would create a massive unphysical force.

Figure 1. shows the original problem setup in a state of deflection when under loading.

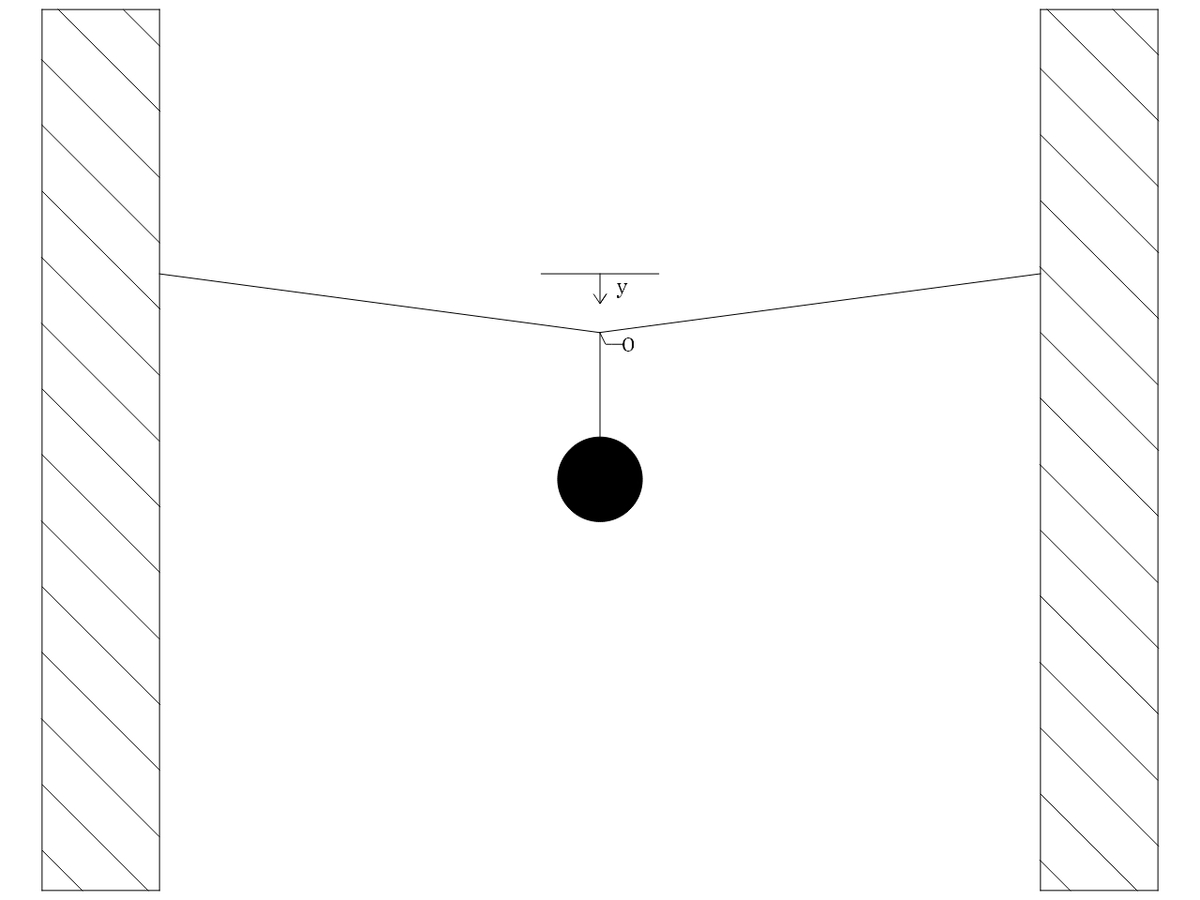$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text {Figure 1}$

The "y" coordinate measures the sag from the horizontal datum to point O.

Begin by summing the forces in the "y" direction, about the point O. Figure 2 is the breakdown of the vector components.

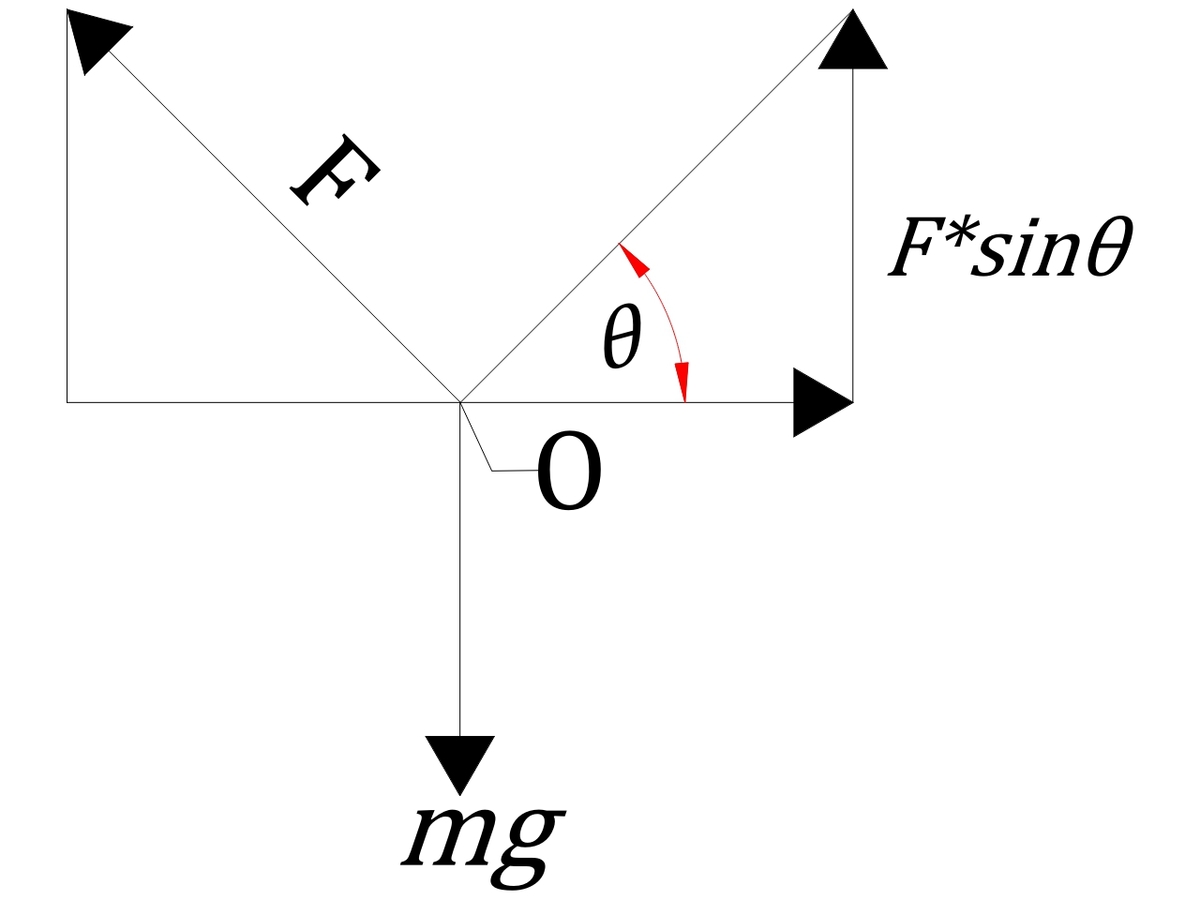$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text {Figure 2}$

$\displaystyle \sum{F_y} = 2Fsin\theta - mg = m\frac{d^2y}{dt^2}$ …Eq1

The position of equilibrium can be found from setting $\displaystyle \frac{d^2y}{dt^2} = 0$

From here the materials stress-strain response must be found. Assuming the string is in the region of deflection where all deformations are elastic, the stress can be related to the strain by the materials Modulus of Elasticity ( assumed constant ) via:

$\displaystyle d\sigma = Ed\epsilon$ ...Eq2

where,

$\displaystyle \sigma$ = Normal Stress

$\displaystyle \epsilon$ = Strain

$\displaystyle E$ = Modulus of Elasticity

or equivalently put, assuming a constant cross-sectional area.

$\displaystyle dF= EAdl/l$ ...Eq3

Next, relate the strain to the angle theta as shown in Figure 3.

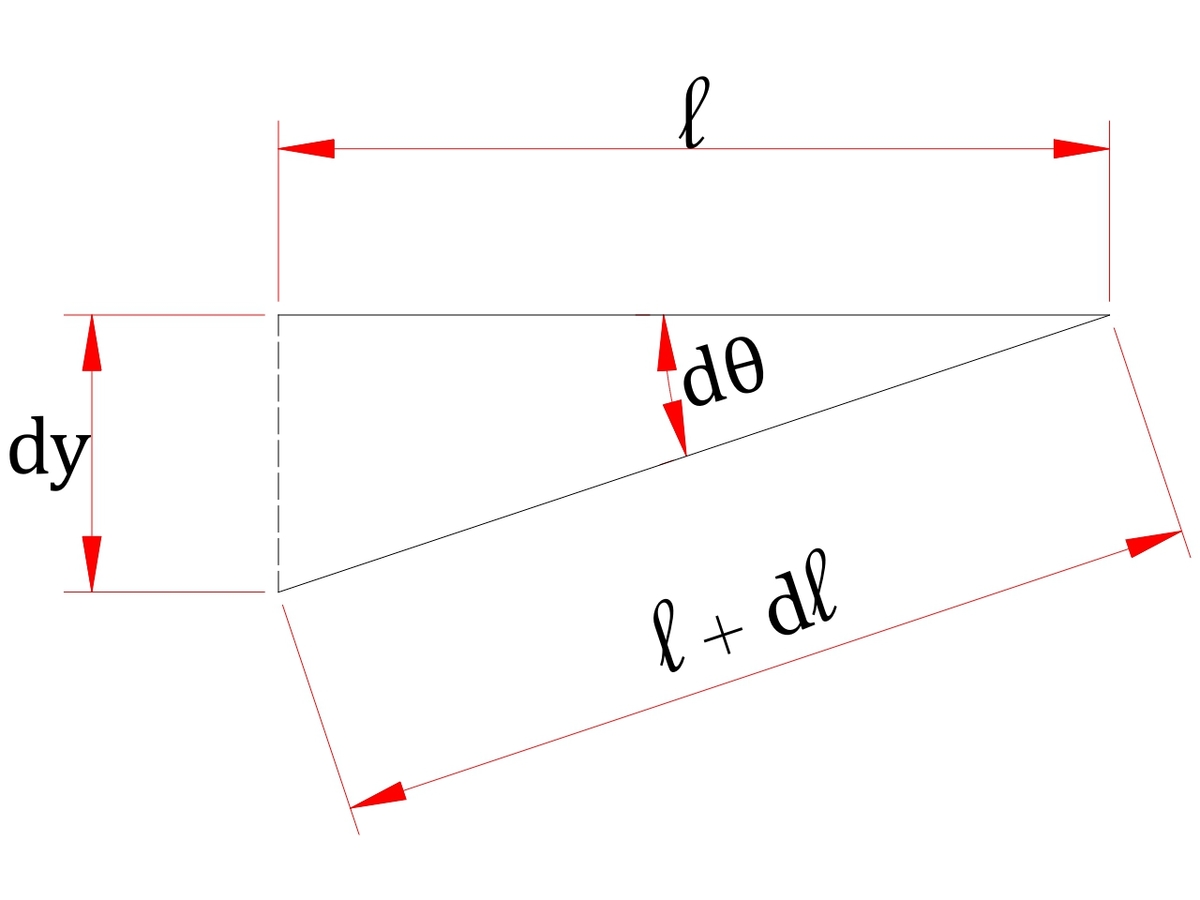$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text {Figure 3}$

Then from vector addition,

$\displaystyle (l + dl) - l = ld\theta \rightarrow \frac{dl}{l} = d\theta$ ...Eq4

Now change variables by substituting Eq4 into Eq3.

$\displaystyle dF= EAd\theta$ ...Eq5.

Integrate Eq5 to give:

$\displaystyle \int_0^F {dF} = EA\int_0^\theta{d\theta} \rightarrow F(\theta) = EA\theta$ ...Eq6

Substitute Eq6 into Eq1' to find the angle of equilibrium.

$\displaystyle 2EA\theta sin\theta - mg = 0$ …Eq7

From here apply the small angle approximation for $sin\theta \approx \theta$ and Eq7 becomes:

$\displaystyle 2EA{\theta}^2 - mg = 0 \rightarrow \theta = \displaystyle\sqrt{\frac{mg}{2EA}}$

Finally, we can go into Eq1 and solve for the tension force $F$ when the system is in static equilibrium:

$\displaystyle F = \frac{mg}{2sin\theta}$ , but now (after the introduction of elasticity) it is apparent that theta has other dependencies (including the mass). So if we want to see what happens when we let the mass tend to zero we can again use the small angle approximation $sin\theta \approx \theta$ and,

$\displaystyle F \approx \frac{mg}{2\theta} =\frac{mg}{2\displaystyle\sqrt{\frac{mg}{2EA}}}$

You can then apply L'Hopital's Rule to find the limit as the mass approaches zero.

$\displaystyle \lim\limits_{m \to 0}F = \lim\limits_{m \to 0} \frac{mg}{2\displaystyle\sqrt{\frac{mg}{2EA}}} =Constant\lim\limits_{m \to 0}\frac{m}{\sqrt{m}} =Constant\lim\limits_{m \to 0}\sqrt{m} = 0$

Most importantly, the relationship shows the tensile force in the supporting ropes are dependent on the materials Modulus of Elasticity. For some MoE, the angle theta may meet or exceed 30 degrees ( ${\theta}^2$ approximates $\theta sin\theta$ well up until about 40 degrees) at which point the forces in all both ropes may be equal and snap, or they angle may exceed 30 degrees and the lower rope may snap. The problem is not stated properly, and no solution can be determined.

The horizontal string will have sheer stress. The vertical string won't.

(We take it as the strings are the same property and density in this problem).. Well they added it. 6dd/8mm/2019

The thing is that in both the strings , the net force is obviously zero . But in the verticle 2 opposite Mg force are canceling each other (one is T1=Mg) And in the case of horizontal string , there are 3 force acting Mg and 2 from the wall . And using 2nd law , you can show that the tension due to wall is , say , T2=Mg/2cos(x) , where x is the angle of depression . SO it is due to this greater forces , the horizontal string should break first.

The tension of the weights are concentrated into a single point of the horizontal string and the vertical has the tension distributed all along it.