String Worldsheet Area
Consider a relativistic string lying on the y-axis at time , stretching from to . The string is parameterized so that one endpoint is at and the other is at , and so that . Now allow the string to propagate from time to time , leaving the string fixed on the y-axis. Find the area of the resulting string worldsheet.
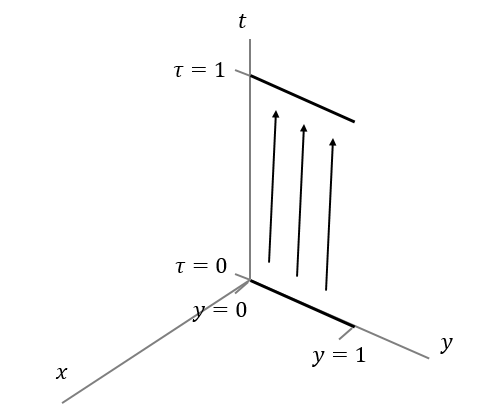
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There is an easy and a hard solution. The easy solution is to recognize that the string worldsheet is a square. Since the string is fixed, the only motion is in the t-direction. After time τ = t = 1 , the worldsheet has length 1 in the t-direction and length 1 in the y-direction. So the worldsheet is square-shaped with side length 1, and thus has area 1.
The hard (but more rigorous) solution is to use the Nambu-Goto action from the String Theory wiki. This uses the Minkowski metric to compute the dot products, which is not discussed in the String Theory wiki in which this problem is found. A string fixed on the y-axis that propagates only in time is parameterized
X μ ( τ , σ ) = ( τ , 0 , σ , 0 ) ,
where the four coordinates here represent the one time and three spatial coordinates. This parameterization comes from the fact that the x and z coordinates are irrelevant (and so are fixed to be 0 ), the time coordinate is equal to τ for the propagation of the string in time, and the string extends along σ in the y-direction.
Computing the partial derivatives for the Nambu-Goto action, one finds:
∂ τ ∂ X μ = ( 1 , 0 , 0 , 0 ) , ∂ σ ∂ X μ = ( 0 , 0 , 1 , 0 ) .
These vectors are clearly orthogonal (even with the Minkowski metric instead of the Euclidean metric), so the first term under the square root in the Nambu-Goto action drops out. Also, both of these vectors have unit norm, although one of them is negative (which one depends on metric convention). So computing the integral in the Nambu-Goto action, we have:
∫ 0 1 d τ ∫ 0 1 d σ ( ∂ τ ∂ X ⋅ ∂ σ ∂ X ) 2 − ( ∂ τ ∂ X ) 2 ( ∂ σ ∂ X ) 2 = ∫ 0 1 ∫ 0 1 d τ d σ − ( − 1 ) ( 1 ) = 1
which is the area of the string worldsheet.