Stringent Numbers 4

Logic Level 1

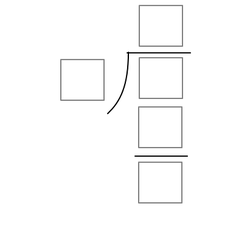The above shows a long division between 2 integers, with the last box at the bottom representing the non-zero remainder of the quotient. Each box represents a distinct single digit positive integer.

Of all the possible solutions, there is only 1 possible value for the remainder of this long division. What is it?

4 3 2 1

2 solutions

Venkatachalam J
Jul 24, 2017

We know that, (Divisor x Quotient) + Remainder = Dividend

From the given condition, Divisor x Quotient≠ Divisor & Divisor x Quotient ≠ Quotient and Divisor ≠ Quotient

So the number 1 is not possible to come in either divisor and quotient place also same numbers are not possible (2 x 2, 3 x 3)

The possible numbers are 2 x 3, 2 x 4, 3 x 2 and 4 x 2 (other combination give two digit result)

For all the combinations the remainder must be 1 otherwise the given condition will not satisfied.

Therefore the only 1 possible value for the remainder is 1.

Mark Lau
Jan 24, 2016

Our goal is construct a possible solution fast and neat. So Consider the upper box of the remainder, probably should not be the divisor, so one may consider quotient=2: so we fastly construct 3*2+1=7 so remainder=1. This is easy to prove that this is the only answer. Interested Reader may prove it by themselves

I mean the only answer-- remainder =1: not the whole division

4 x 2 + 1 = 9

Pi Han Goh - 5 years, 4 months ago

Stringent Numbers 4

2 solutions

0 pending reports