Strong bonds
Which twodimensional molecule is most stable?
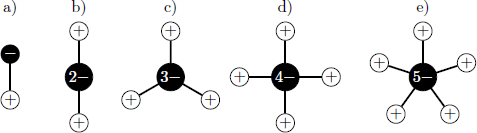
Details and Assumptions:
- Each bond has the same length.
- The bond angle is with the coordination number .
- Treat the atoms as point charges.
- Consider the electrostatic energy for a single hydrogen atom.
Bonus question: What would change if the molecules could also extend to the third dimension?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The electrostatic energy reads V = 4 π ε 1 j = 1 ∑ n ∣ r 0 − r j ∣ q 0 q j = 4 π ε d e 2 z n [ j = 1 ∑ n − 1 r 0 j 1 − n ] with the bond lenght d , elemental charge e , the coordination number n and the relative distance r 0 j (in units of d ). We evaluate the dimensionless factor z n for each molecule: z 1 z 2 z 3 z 4 z 5 = − 1 = 2 1 − 2 = − 1 . 5 = 3 1 + 3 1 − 3 ≈ − 1 . 8 5 = 2 1 + 2 1 + 2 1 − 4 ≈ − 2 . 5 9 = 2 sin ( 3 6 ∘ ) 1 + 2 sin ( 3 6 ∘ ) 1 + 2 sin ( 7 2 ∘ ) 1 + 2 sin ( 7 2 ∘ ) 1 − 5 ≈ − 2 . 2 5 Therefore, the case n = 4 is energetically most favourable.