Stubborn rod, it don't wanna move.....

Classical Mechanics Level 4

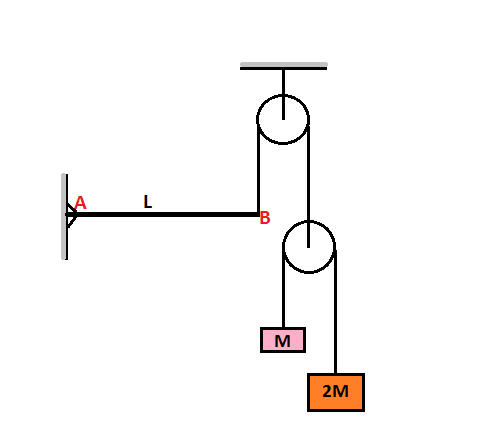Consider the situation shown in the figure. Uniform rod $AB$ of length $L$ can rotate freely about the hinge $A$ in vertical plane. Pulleys and strings are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of rod is ->

Find more here

\frac{32M}{3}

\frac{8M}{5}

\frac{4M}{5}

\frac{16M}{3}

\frac{8M}{3}

\frac{4M}{3}

2 solutions

Aniket Verma
Mar 5, 2015

$2Mg - T = 2Ma$ ----> $1$

$T - Mg = Ma$ -----> $2$

where $T =$ tension in the string connected two the hanging masses, and $a =$ their acceleration.

Adding $1 \& 2$

we get $a = \dfrac{g}{3}$ and $T = \dfrac{4Mg}{3}$

let mass of the rod $AB$ be $m$

now balance the torque on the rod $AB$ about point $A$ .

$\dfrac{mgL}{2} = 2TL$ (we have taken $2T$ force at end $B$ because the string connected to the rod is acted upon by $T$ on the both side of the $2_{nd}$ pulley)

$\Rightarrow$ $\dfrac{mgL}{2} = \dfrac{8MgL}{3}$

therefore $m = \dfrac{16M}{3}$

My working was similar to yours, except that I took the force at end B to be T. Why is it 2T?

Aran Pasupathy - 5 years, 11 months ago

weight of rod is supported by the second pulley which hangs masses M and 2M, therefore tension will be twice at the peg

Syed Baqir - 5 years, 11 months ago

Aakash Khandelwal
Apr 1, 2016

After proper analysis , we find that both masses move with accelaration of magnitude $g/3$ .

Thus tension $T$ in the pulley containing rope attatched to rod= $8Mg/3$ .

Therefore $\tau_{net} =0$ about hinge.

Hence $m= 16M/3$

Stubborn rod, it don't wanna move.....

2 solutions

0 pending reports