Subdivided triangle
A triangle is subdivided into 25 smaller triangles as shown in the figure below. Two of these 25 triangles are selected at random. The probability that the two selected triangles have exactly one vertex in common can be expressed as b a where a and b are coprime positive integers. What is the value of a + b ?
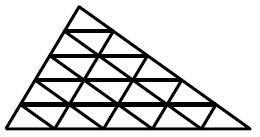
The answer is 61.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Can you come up with another way of counting these possible pairs?
what i don't understand is.. what is neighbour and vertex? that's why i can't answer this maybe..
Log in to reply
May be I should have explained: `neighbor' is not a mathematical word. Two different small triangles are neighbors if they have something in common: a vertex (an angle of a triangle) or an edge (a side of a triangle). Hope this helps.
To allow discussion, we number the triangles from top to bottom and left to right, from 1 to 2 5 . Consider the nine hexagons formed by groups of six triangles (for example, the hexagon of triangles 2 , 3 , 4 , 6 , 7 , 8 ). For each of 6 triangles in a certain hexagon, there are 3 other triangles also in the hexagon that share only a vertex with it (for example, triangles 4 , 7 , 8 share only a vertex with triangle 2 ). Thus, in each hexagon, there are 2 1 ⋅ 6 ⋅ 3 = 9 pairs of triangles that share only a vertex. (Here we divide by 2 to account for the fact that each pair is originally counted twice: once for each triangle.)
We see that there are 6 hexagons in the figure, so there are 9 ⋅ 6 = 5 4 pairs of triangles that are both in a certain hexagon. However, we also have to account for the pairs that are not in a hexagon (such as triangles 2 and 5 ). These can be only be between two triangles on the very edge of the figure, so we can easily count 1 2 pairs of triangles in this case. Thus, in total, there are 5 4 + 1 2 = 6 6 pairs of triangles only sharing a vertex, and the requested probability is ( 2 2 5 ) 6 6 = 5 0 1 1 . The answer is 1 1 + 5 0 = 6 1 .
We have two types of vertex. One is the vertexes shared by 3 triangle ( there are 12 of them on edges of the big triangle). The other is the vertexes shared by 6 triangle (there are 6 of them inside the big triangle). For type 1: each vertex has only one choice to select two triangles having exactly one common vertex. For type 2: each vertex has 9 choices. The number 9 can be figured out by 6C2 - 6 ( the total number of arrangements - the number of pairs of triangle that share an edge) Therefore the probability is \frac{( 12+6*9)}{25C2} = \frac{11}{50} So, a+b = 11+50 +61
In the large triangle, there are 6 distinct triangle positions:
-
The small triangles on the big triangle's vertices The 3 small triangles on the vertices of the large one have 2 other such triangles that they share exactly one vertex with. So, the probability of two triangles sharing exactly one vertex given the first triangle is on one of the big triangle's vertices is 2/24.
-
Small triangle with exactly one base on the side of the big triangle. There are 9 such small triangles, and by counting each has 5 other small triangles with whom they share exactly one vertex. So, given that one of these triangles is one of the small triangles selected, the probability that the two share exactly one vertex is 5/24.
-
Small triangles that share one side with the triangles from case 1 There are 3 such small triangles, and by counting each has 3 other small triangles with whom they share exactly one vertex. So, given that one of these triangles is one of the small triangles selected, the probability that the two share exactly one vertex is 3/24.
-
Small triangles with exactly one vertex on a side of the big triangle There are 6 such small triangles, 2 on each side, and by counting each has 6 other small triangles with whom they share exactly one vertex. So, given that one of these triangles is one of the small triangles selected, the probability that the two share exactly one vertex is 6/24.
-
The small triangle in the center of the big triangle There is only 1 such triangle, and by counting it has 9 other small triangles with whom it shares exactly one vertex. So, given that this triangle is one of the small triangles selected, the probability that the two share exactly one vertex is 9/24.
-
Small triangles that share a side with the center triangle from case 5 There are 3 such small triangles, and by counting each has 9 other small triangles with whom they share exactly one vertex. So, given that one of these triangles is one of the small triangles selected, the probability that the two share exactly one vertex is 9/24.
Now, by combining all the cases, the desired probability is the sum of the probabilities of each case occurring. So, the desired probability is (3/25) * (2/24) + (9/25) * (5/24) + (3/25) * (3/24) + (6/25) * (6/24) + (1/25) * (9/24) + (3/25) * (9/24) = (1/(25*24)) * (6 + 45 + 9 + 36 + 27 + 9) = 132/600 = 11/50.
So, a + b = 11 + 50 = 61
There are five different types of small triangles.
There are 3 triangles in a corner: each of them has 2 neighbors with one vertex in common.
There are 3 triangles opposite the corner triangle: each of them has 3 neighbors with one vertex in common.
There are 9 triangles with two vertices on the edge of the big triangle: each of them has 5 neighbors with one vertex in common.
There are 6 triangles with one vertex on the edge of the big triangle: each of them has 6 neighbors with one vertex in common.
There are 4 triangles with no vertex on the edge of the big triangle each of these has 9 neighbors with one vertex in common.
In total this sums up to 132 pairs with one vertex in common. We counted each pair two times, so there are 66 pairs. There are 2 5 C 2 = 3 0 0 pairs of triangles, so P ( one vertex in common ) = 3 0 0 6 6 = 5 0 1 1 .