Submerged Sphere Plugging Hole
There is a sphere of radius R with its bottom part plugging a hole of radius r , where R r = 4 3 . The hole is at the bottom of a water container, and the water container is filled to an arbitrary depth.
There is some minimum sphere weight such that the sphere does not float upward, regardless of the height of the water in the container. This is equivalent to the maximum buoyant force that the sphere could be subjected to. Call this minimum sphere weight W m i n .
Define another quantity W r e f = 3 4 π R 3 ρ g , where ρ is the water density and g is the ambient gravitational acceleration. W r e f is the weight of water that the sphere would displace if it was entirely surrounded by water.
Determine the following ratio:
W r e f W m i n = ?
Note:
This was inspired by a question posed by
Azimuddin Sheikh
Note:
Neglect atmospheric (air) pressure
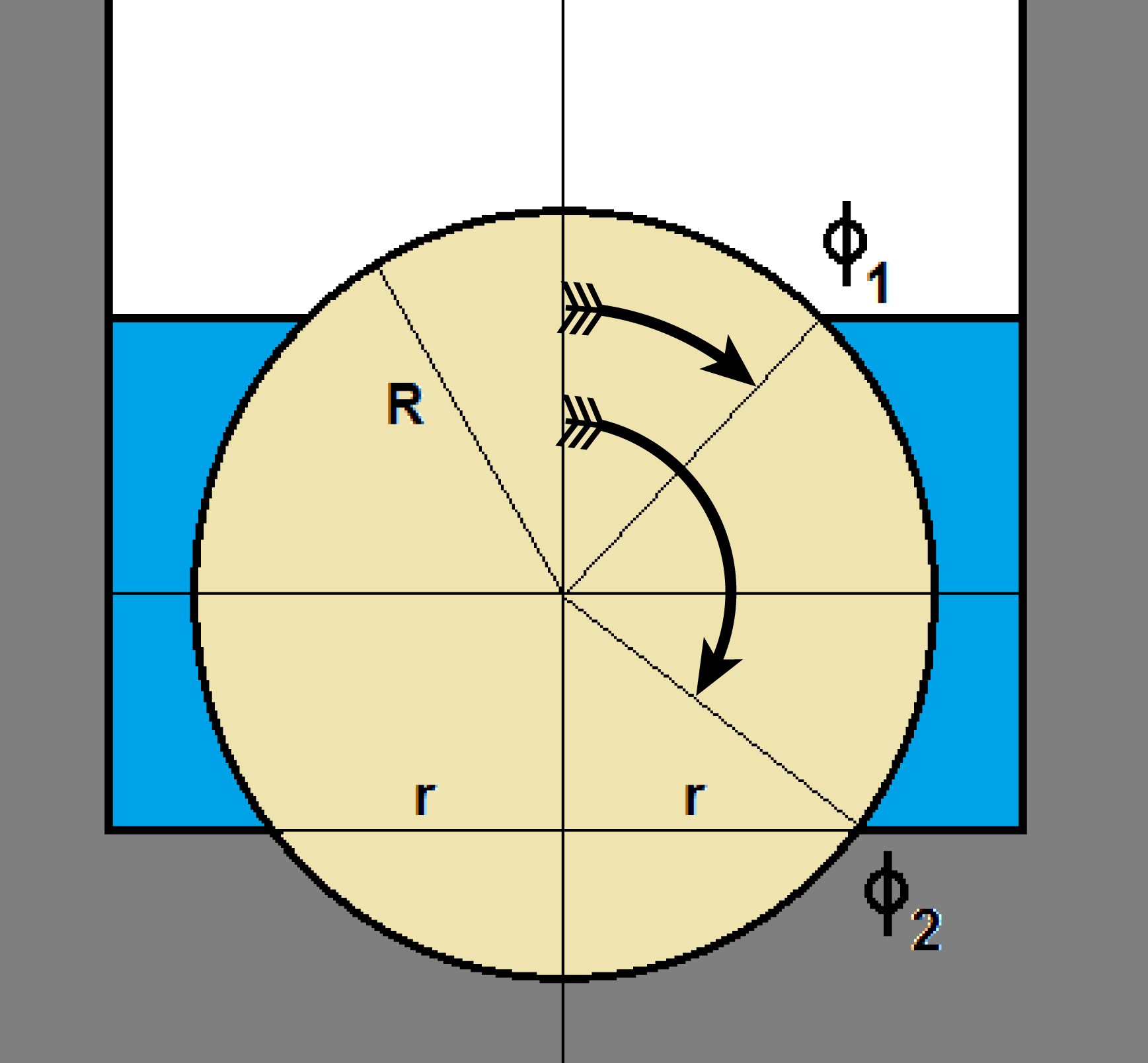
The answer is 0.289379.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
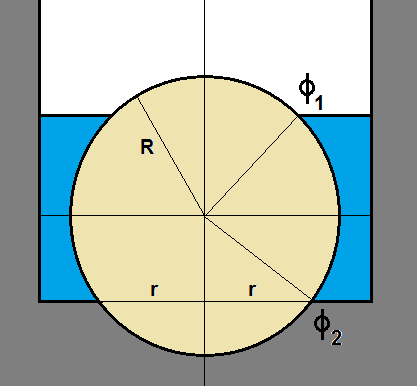
The sphere of radius R sits in a hole of radius r at the bottom of a container. Suppose that the center of the sphere is at the origin ( x , y , z ) = ( 0 , 0 , 0 ) . Let ϕ be the angle with respect to the positive z axis, and let θ be the angle with respect to the positive x axis.
Water fills the container from the bottom to some height. Let ϕ 2 correspond to the bottom contact point between the water and the sphere, and let ϕ 1 correspond to the top contact point between the water and the sphere.
The expression for ϕ 2 in terms of r and R is:
ϕ 2 = 2 π + a c o s ( R r )
The expression for the z coordinate of an arbitrary point on the sphere is:
z = R c o s ( ϕ )
Here, ϕ = 0 corresponds to the top of the sphere. The pressure is:
P = ρ g R [ c o s ϕ 1 − c o s ϕ ]
The infinitesimal sphere surface area is:
d A = R 2 s i n ϕ d θ d ϕ
The infinitesimal pressure force magnitude is:
d F = P d A = ρ g R 3 s i n ϕ [ c o s ϕ 1 − c o s ϕ ] d θ d ϕ
The infinitesimal force in the z direction is:
d F z = d F R − z = d F ( − c o s ϕ ) = − ρ g R 3 s i n ϕ c o s ϕ [ c o s ϕ 1 − c o s ϕ ] d θ d ϕ
The total force in the z direction is:
F z = − ρ g R 3 ∫ ϕ 1 ϕ 2 ∫ 0 2 π s i n ϕ c o s ϕ [ c o s ϕ 1 − c o s ϕ ] d θ d ϕ = − 2 π ρ g R 3 ∫ ϕ 1 ϕ 2 s i n ϕ c o s ϕ [ c o s ϕ 1 − c o s ϕ ] d ϕ = − 3 π ρ g R 3 [ c o s ϕ 1 − c o s ϕ 2 ] 2 [ c o s ϕ 1 + 2 c o s ϕ 2 ]
As a sanity check, suppose the hole had zero width, and that the water was filled to the top of the sphere. In this case, ϕ 1 = 0 and ϕ 2 = π . The F z expression reduces to:
F z = − 3 π ρ g R 3 [ 1 + 1 ] 2 [ 1 − 2 ] = 3 4 π ρ g R 3 = V s p h e r e ρ g = weight of displaced water
In general, we take ϕ 2 as a given, and we must find the value of ϕ 1 which maximizes the upward pressure force. I will leave this as an exercise for the reader, but it turns out that the upward pressure force is maximized when the following condition is satisfied:
ϕ 1 + ϕ 2 = π
So the minimum weight of the sphere, to ensure that it covers the hole unconditionally, is:
W s p h e r e − m i n = − 3 π ρ g R 3 [ c o s ϕ 1 − c o s ϕ 2 ] 2 [ c o s ϕ 1 + 2 c o s ϕ 2 ] ϕ 2 = 2 π + a c o s ( R r ) ϕ 1 = π − ϕ 2 = 2 π − a c o s ( R r )
Noting that water can be treated under such conditions as present in this problem as being an incompressible, homogeneous fluid and making the assumption that for the purposes of this problem that gravitational field is vertical and uniform, the minimum weight of the sphere to provide neutral bouyancy, ignoring any buoyancy from the portion that is in air (should we assume vacuum conditions), per Archimedes' principle as stated in his book On Floating Bodies prepositions 3 through 7 , is the weight of the water displaced by the fraction of the sphere submerged in water. That minimum weight that satisfies the condition of regardless of water depth is when the sphere is fully submerged sitting in the position described in this problem. Since, ρ , g and R factor out in the weight ratio, set them all to 1. Solving for h using the Pythagorean Theorem and ignoring the unusable solution, h ⟹ 4 1 ( 4 − 7 ) . Using the spherical cap formula, the volume of the spherical cap is 4 8 1 ( 4 − 7 ) 2 ( 4 1 ( 7 − 4 ) + 3 ) π . The, we we want to computer the faction of the sphere that is submerged as that is the desired weight ratio, 1 − 3 4 π v ⟹ 1 − 6 4 1 ( 4 − 7 ) 2 ( 4 1 ( 7 − 4 ) + 3 ) ≈ 0 . 9 2 3 7 3 3 6 0 8 4 1 2 6 8 8 .
I do not see how the angle you computed is the desired answer.
Having said all that, I do realize that this is an except to Archimedes' Principle known as the bottom case . Please, see Using surface integrals for checking the Archimedes’ law of buoyancy . In which case, there is no minimum weight for the sphere as the buoyancy is always negative (downward).
I have added a note stating to neglect atmospheric pressure. Regarding the maximum buoyant force, my intuition was initially the same as yours; that the maximum upward force from the fluid will occur when the sphere is fully submerged. But then upon checking that intuition by doing the integral, I found that not to be the case. Here is an intuitive argument summarizing the results:
1)
If the water level is below the sphere diameter, all fluid forces point upward, so the "optimum" water level can't be any lower than that.
2)
As the water level rises above the diameter, the upward pressure forces (on the bottom half of the sphere) get stronger because of the increased water depth.
3)
As the water level rises above the diameter, downward pressure forces start to accumulate (on the upper half of the sphere)
Points (2) and (3) are at odds with each other, effectively giving us an optimization problem to solve. As it turns out, the two ϕ values need to be equidistant from 2 π , with the deviation from 2 π depending on the ratio of the hole radius to the sphere radius. For a hole radius of zero, we're back to the standard intuition, as I showed in my "sanity check". 'Tis a fascinating subject
Log in to reply
I edited my previous comment please review.
Log in to reply
I posted a problem on the "bottom case" a few weeks ago.
https://brilliant.org/problems/buoyant-force-2/?ref_id=1558794
The problem under consideration here is less trivial than the "bottom case". It is a proper optimization problem.
I opine that your answer is wrong. So far, I have seen nothing to cause me to change my opinion. Considering the bottom case, which did catch me by surprise , the only way to get an upward buoyancy force is for the water level to be such that Φ 1 ≤ − Φ 2 where the angles are measured from the horizontal mid level of the sphere in a counterclockwise manner and that the minimum weight of sphere is dependent on the water depth and goes down as the water level does down so that the minimum weight is reached a zero water depth. The maximum buoyancy is reached when the water is at the mid level of the sphere and then the weight needs to be at most the weight of the mass of the water displaced. That problem is a maximization, not a minimization, and still has a different answer.
I contend that the buoyant force is not maximized when the water level reaches the middle of the sphere. While it is true that the we begin to accumulate downward forces after that point, the upward forces from the bottom half of the sphere are also getting stronger. These two effects "fight" each other, and as a consequence, the net upward force is maximized when the water level is somewhere between the middle of the sphere and the top. In addition to the hand analysis presented above, I made computer program to calculate the double-integral representing the overall upward force. The two agree. Also, I am asking for the minimum weight of the sphere, such that the buoyant force never exceeds that weight under any circumstances.
Using your formula (F_z=g (-\rho ) R^3 \int _{\phi _1}^{\phi _2}\int _0^{2 \pi }\sin (\phi ) \cos (\phi ) \left(\cos \left(\phi _1\right)-\cos (\phi )\right)d\theta d\phi), the following modifications: the inner integral is merely a multiplication of 2 π , it saves effort to substitute for c o s ( ϕ 1 ) = − cos − 1 ( 4 3 ) immediately and the constants before the first integral disappear in the final W r e f W m i n .
∫ − cos − 1 ( 4 3 ) ϕ 2 sin ( ϕ ) cos ( ϕ ) ( 4 3 − cos ( ϕ ) ) d ϕ ⟹ 3 8 4 1 ( 3 − 4 cos ( ϕ 2 ) ) 2 ( 8 cos ( ϕ 2 ) + 3 )
∂ ϕ ∂ ( 3 8 4 1 ( 3 − 4 cos ( ϕ ) ) 2 ( 8 cos ( ϕ ) + 3 ) ) = 0 ∧ − cos − 1 ( 4 3 ) ≤ ϕ ≤ 2 π ⟹ { ϕ → 0 } , { ϕ → 2 π } , { ϕ → − cos − 1 ( 4 3 ) } , { ϕ → cos − 1 ( 4 3 ) } .
The second derivative is − 4 8 1 cos ( ϕ ) ( 3 − 4 cos ( ϕ ) ) 2 + 4 8 1 cos ( ϕ ) ( 8 cos ( ϕ ) + 3 ) ( 3 − 4 cos ( ϕ ) ) − 3 1 sin 2 ( ϕ ) ( 3 − 4 cos ( ϕ ) ) + 1 2 1 sin 2 ( ϕ ) ( 8 cos ( ϕ ) + 3 ) ) evaluated at the previously mentioned inflection points gives − 4 1 , − 4 3 , 6 4 2 1 , 6 4 2 1
Therefor the maximum buoyancy occurs at ϕ 2 = 2 π . There is a local maximum at the sphere's mid level and two local minima where the cosine of the angle is (\frac34).
I think we are using different conventions for ϕ . I am measuring it from the vertical. So the top of the sphere is ϕ = 0 . Also, ϕ 2 is fixed at 2 π + a c o s ( 3 / 4 ) , and is not variable (when using my formula, at least). ϕ 1 (when using my equation) is the only thing that varies.
Log in to reply

I suggest editting your problem and replacing the image.
Log in to reply
Thanks. I have replaced the image. Regarding the physics, are we still at an impasse?
Point 1: The inner integration is just a multiplication by 2 π .
Your original formula, with the subscripted ϕ replaced with other Greek letters: F z = g ( − ρ ) R 3 ∫ α β ∫ 0 2 π sin ( ϕ ) cos ( ϕ ) ( cos ( γ ) − cos ( ϕ ) ) d θ d ϕ ⟹ 6 1 π g ρ R 3 ( − 3 cos ( 2 α ) cos ( γ ) + 4 cos 3 ( α ) + 3 cos ( 2 β ) cos ( γ ) − 4 cos 3 ( β ) ) .
Your original formula with the inner integral removed and 2 π placed in front: F z = − 2 π g ρ R 3 ∫ α β sin ( ϕ ) cos ( ϕ ) ( cos ( γ ) − cos ( ϕ ) ) d ϕ ⟹ − 2 π g ρ R 3 ( 4 1 cos ( γ ) ( cos ( 2 α ) − cos ( 2 β ) ) + 3 1 ( cos 3 ( β ) − cos 3 ( α ) ) ) .
The two result may not resemble each other; but, they have the same value: 6 1 π g ρ R 3 ( − 3 cos ( 2 α ) cos ( γ ) + 4 cos 3 ( α ) + 3 cos ( 2 β ) cos ( γ ) − 4 cos 3 ( β ) ) = − 2 π g ρ R 3 ( 4 1 cos ( γ ) ( cos ( 2 α ) − cos ( 2 β ) ) + 3 1 ( cos 3 ( β ) − cos 3 ( α ) ) ) ⟹ True
Point 2:
p h i 2 is π − sin − 1 ( 4 3 ) radians, about 1 3 1 . 4 1 ∘ .
Subtituting α for p h i 2 because Wolfram has issues with subscripted variable names and the constants not present as they do not affect the final result, ∫ α π − sin − 1 ( 4 3 ) sin ( ϕ ) cos ( ϕ ) ( cos ( α ) − cos ( ϕ ) ) d ϕ ⟹ 1 9 2 1 ( − 1 8 cos ( α ) + 8 cos ( 3 α ) − 7 7 ) .
∂ α ∂ ( 1 9 2 1 ( − 1 8 cos ( α ) + 8 cos ( 3 α ) − 7 7 ) ) = 0 ∧ 0 ≤ α ≤ π − sin − 1 ( 4 3 ) ⟹ { α → 0 } , { α → 2 tan − 1 ( 3 1 ( 4 − 7 ) ) } , { α → 2 tan − 1 ( 3 1 ( 7 + 4 ) ) }
The α values are where the sine of angle is 0 or 0.75. The minimum occurs at the middle value in the list.
Point 3:
I am not happy with my previous answer. Therefore, I reworked it from the beginning. This answer matches my understanding of the bottom case situation. This time I am using colatitudes from the "north pole" (upper z axis position). I am using vector analysis to set up the integral and applying the necessary correction for integrating in spherical coordinates. This last point is what I previously did incorrectly. I retained your meanings for ϕ and θ . I reversed the order of the integration limits on the remaining integral. That only causes a negation of the result. Because colatitudes are being used, the formula for ϕ 2 has to use arcsin and not arccos . I used a vector dot product to extract the buoyancy force from the direction cosines and sued the fact that on a unit sphere the unit normals to the surface are the Cartesian point coordinates.
I am assuming a radius of 1 because that also scales out of the problem.
mapping = CoordinateTransformData [ Spherical → Cartesian , Mapping , { 1 , ϕ , θ } ] ⟹ { cos ( θ ) sin ( ϕ ) , sin ( θ ) sin ( ϕ ) , cos ( ϕ ) }
The following is the necessary correction for integrating in spherical coordinates:
jacobian = CoordinateTransformData [ Spherical → Cartesian , MappingJacobianDeterminant , { 1 , ϕ , θ } ] sin ( ϕ )
Now, I do the integration both with the inner integral and with the inner integral replaced by a factor of 2 π :
∫ π − sin − 1 ( 4 3 ) α ( ∫ 0 2 π { 0 , 0 , 1 } . mapping d θ ) jacobian d ϕ ⟹ − 1 6 1 π ( 8 cos ( 2 α ) + 1 )
2 π ∫ π − sin − 1 ( 4 3 ) α { 0 , 0 , 1 } . mapping jacobian d ϕ ⟹ − 1 6 1 π ( 8 cos ( 2 α ) + 1 )
Now to locate the extrema: ∂ α ∂ ( − 1 6 1 π ( 8 cos ( 2 α ) + 1 ) ) = 0 ∧ 0 ≤ α ≤ π − sin − 1 ( 4 3 ) ⟹ { α → 0 } , { α → 2 π } . Examining the second derivatives, the first in a minimum and the second is a maximum.
− 1 6 1 π ( 8 cos ( 2 α ) + 1 ) /. { { α → 0 } , { α → 2 π } } ⟹ { − 1 6 1 ( 9 π ) , 1 6 7 π } .
Normalizing to the volume of the entire sphere: 3 1 6 ( 4 π ) 7 π = 6 4 2 1 = 0 . 3 2 8 1 2 5
Later update: pressure due to depth was omitted. Correct answer is further down. I deliberately left this discussion in place as a lesson to others.
Log in to reply
Regarding Point 3, where is the pressure function incorporated into the integral?
I'm going through this piece by piece. For your Point 2, we do indeed want the minimum (negative) value, since there is a negative multiplier for the integral. Your second value for alpha matches my optimal value for ϕ 1 , which turns out to be 2 π − a c o s ( 3 / 4 ) . So I agree with your analysis of my integral in Point 2
See Point 3: above to understand the framework. My disagreement had come from not understanding his angles and from where they were measured. This reworking includes the pressure due to depth, which I had omitted in Point 3 above. mapping and jacobian are unchanged from above.
∫ π − sin − 1 ( 4 3 ) α ( ∫ 0 2 π ( cos ( α ) − cos ( ϕ ) ) { 0 , 0 , 1 } . mapping jacobian d θ ) d ϕ = 2 π ∫ π − sin − 1 ( 4 3 ) α ( cos ( α ) − cos ( ϕ ) ) { 0 , 0 , 1 } . mapping jacobian d ϕ ⟹ 9 6 1 π ( 1 8 cos ( α ) − 8 cos ( 3 α ) + 7 7 )
∂ α ∂ ( 9 6 1 π ( 1 8 cos ( α ) − 8 cos ( 3 α ) + 7 7 ) ) = 0 ∧ 0 ≤ α ≤ π − sin − 1 ( 4 3 ) ⟹ { α → 0 } , { α → 2 tan − 1 ( 3 1 ( 4 − 7 ) ) } , { α → 2 tan − 1 ( 3 1 ( 7 + 4 ) ) }
The second derivative shows that first and last α values are minima and the middle value is the only maxima.
Those extrema, normalize to the volume of the complete sphere are: { 1 2 8 1 ( 7 7 + 1 0 ) , 6 4 7 7 , 0 } ≈ { 0 . 2 2 2 8 1 4 5 2 4 8 2 3 8 4 5 , 0 . 2 8 9 3 7 9 0 4 9 6 4 7 6 9 , 0 . } .
The maximum buoyancy (the middle number, identified as the maximum) has to be counteracted. The minimum weight that would suffice is the same amount.
It looks like we are finally in agreement, assuming that your middle number is the answer
You need to counteract the maximum buoyancy, which is the minimum weight that would suffice to keep the sphere in place.
A well-known fact is that buoyant force is equal to the weight of the displaced water volume. The fact that the bottom of the sphere is sticking out might complicate things however.
Let's first look at the situation that there is no hole and the water extends below the sphere.
If the water level is at distance a below the top of the sphere, the submerged volume is V = ∫ − a + R R π ( R 2 − x 2 ) d x = π ( 3 4 R 3 − R a 2 + 3 1 a 3 ) and the buoyant force would be ρ g V .
But above we assumed the bottom of the sphere was submerged, while in fact it is plugging the hole. So we will have to subtract the 'plugging force': the pressure at the level of the hole, times its area. Yes, this is exactly the upward force that we are missing out ow, compared to the previous case (after all, a flat-bottomed 'sphere'of the same weight would have done the same job).
Suppose the sphere extends a distance d below the plug hole, then the depth of the hole below the surface equals 2 R − a − d , so that the pressure is P = ρ g ( 2 R − a − d ) while we are plugging an area A = π r 2 = π ( 2 R d − d 2 ) , and the force is F h o l e = P A = ρ g π ( 4 R 2 d − 4 R d 2 − 2 R d a + a d 2 − d 3 ) .
The net buoyant force then is F = ρ g V − F h o l e = ρ g π ( 3 4 R 3 − R a 2 + 3 1 a 3 − 4 R 2 d + 2 a R d + 4 R d 2 − a d 2 − d 3 )
The value of a for maximum force is found by setting the derivative of this expression with respect to a to 0:
a 2 − 2 R a + 2 R d − d 2 = 0 ⇒ a = R ± R 2 − 2 R d + d 2 = R ± ( R − d ) .
One solution, a = 2 R − d , corresponds to a minimum since there is no water at all; the other, a = d , corresponds to maximum buoyant force, which then becomes
F m a x = ρ g π ( 3 4 R 3 − 4 R 2 d + 5 R d 2 − 3 5 d 3 ) .
Using a substitution d = α R , we get
F m a x = 3 4 ρ g π R 3 ( 1 − 3 α + 4 1 5 α 2 − 4 5 α 3 ) .
(Using Pythagoras, we have α = 1 − 4 1 7
F m a x = W m i n = W r e f • 0 . 2 9 4 5 8 7 7 0 4 .
Below are my notes, with a scetch to clarify my use of a , d and α .