Substitute or visualise?
Find the value of the expression:
n = 1 ∑ ∞ ( 4 1 ) n
If your answer is in the form b a where a and b are co-prime positive integers, then what is a + b ?
This problem in not original.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice animation. In my mind I was imagining this with squares, but triangles work just as well.
I was thinking of referencing the exact same video from Think Twice while solving the problem!!
The same problem was discussed by David Acheson in his book “The Calculus story”. So I remembered the answer. Also we can solve it by using the formula for the sum of the terms of an infinite GP(a/1-r)
n = 1 ∑ ∞ ( 4 1 ) n = n = 0 ∑ ∞ ( 4 1 ) n − 1 = 1 − 4 1 1 − 1 = 4 3 1 − 1 = 3 4 − 1 = 3 1
Typo in last line:1/3
Log in to reply
Thank you!
Let S n be the answer
S n = n = 1 ∑ ∞ = 4 1 + 1 6 1 + 6 4 1 . . .
4 1 S n = 1 6 1 + 6 4 1 + 2 5 6 1 . . .
S n ( 1 − 4 1 ) = 4 1
S n ( 4 3 ) = 4 1
S n = 4 1 × 3 4 = 3 1
As H C F ( 1 , 3 ) = 1 therefore answer is 3 + 1 = 4
Use the geometric series formula:
a ∑ n = 0 ∞ r n = 1 − r a .
Here a = r = 4 1 , so the sum is ( 4 1 ) ( 3 4 ) = 3 1 .
Substitution method:
Let S = ∑ n = 1 ∞ 4 n 1 .
Then 4 S = ∑ n = 0 ∞ 4 n 1 = 1 + ∑ n = 1 ∞ 4 n 1 ,
so 4 S − 1 = S . I.e., S = 3 1 .
I'll leave the visual proof for somebody else. It makes a nice picture.
I have already shown it in mine! Do watch it!
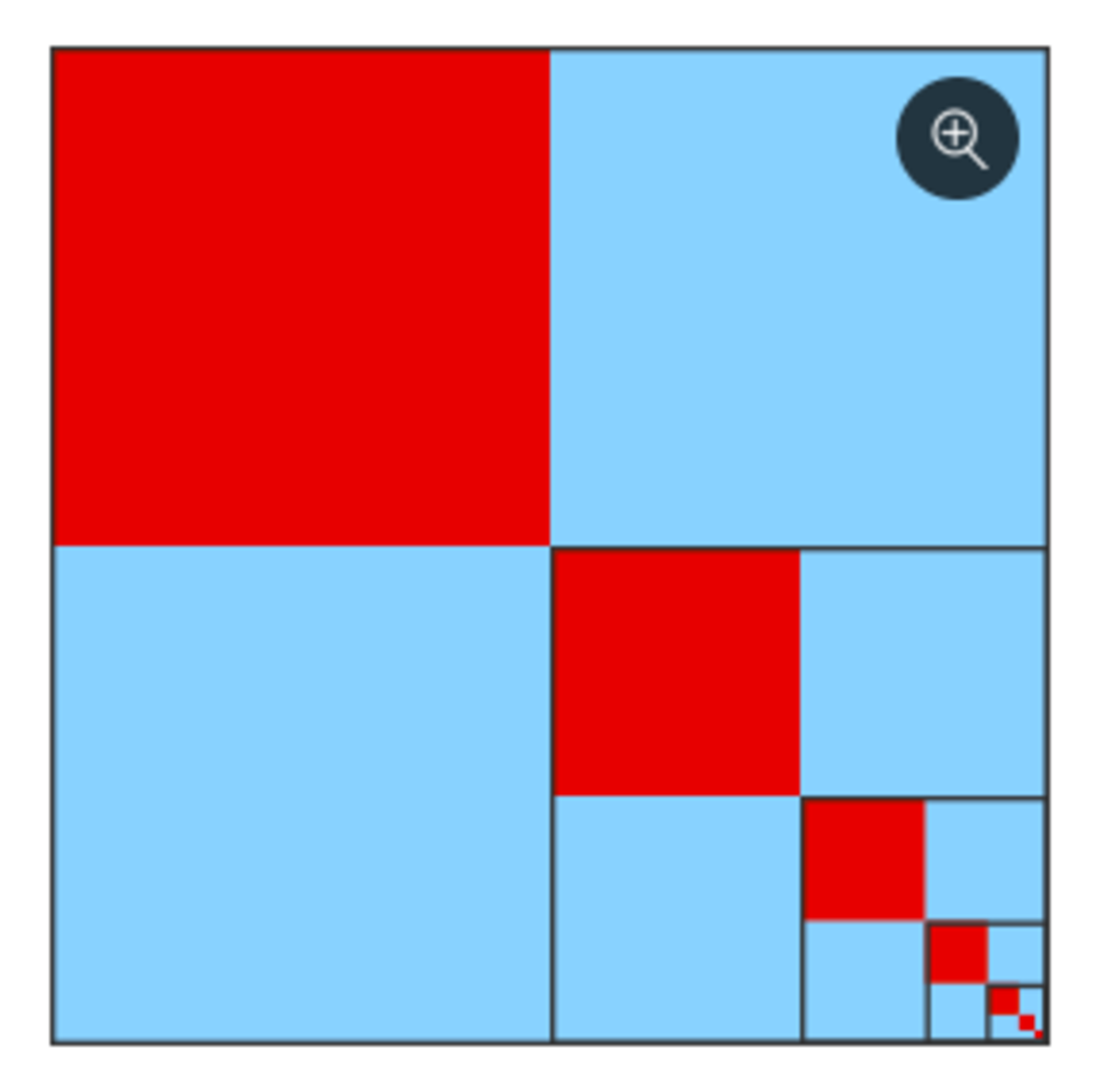
Visual approach:
Video link
⟹ x = 3 1
⟹ a = 1 , b = 3
⟹ a + b = 4
Algebraic approach:
x = n = 1 ∑ ∞ 4 n 1 = 4 1 + 4 2 1 + 4 3 1 ⋯
⟹ 4 x = 1 + 4 1 + 4 2 1 + 4 3 1 ⋯
⟹ 4 x − 1 = 4 1 + 4 2 1 + 4 3 1 ⋯ = x
⟹ 4 x − 1 = x ⟹ 3 x = 1 ⟹ x = 3 1
⟹ a = 1 , b = 3
⟹ a + b = 4