Substrings in powers

First we prove the following: If $\log_{10}p$ is an irrational number then $N_p(n) < \infty$ for every $n \in \N$ .

In order to prove it we will show that for every $n \in \N$ there exists an exponent $k_0 \in \N$ , such that the value $p^{k_0}$ begins with n (i.e. the first digits of the number $p^{k_0}$ are the same as $n$ ).

Indeed, let $n \in \N$ have the form $d_1 d_2 \ldots d_l$ (for example, if $n = 492$ , then $d_1 = 4$ , $d_2 = 9$ , $d_3 = 2$ , $l = 3$ ). Note that, if $\alpha \in \left[\log_{10} d_1.d_2 \ldots d_l, \log_{10}d_1.d_2 \ldots d_l 9 \right) \subseteq [0, 1]$ , then $10^\alpha \in \left[d_1.d_2 \ldots d_l, d_1.d_2 \ldots d_l 9 \right)$ (for example, if $n=492$ , then $d_1.d_2d_3$ represents $4.92$ and $d_1.d_2d_3 9$ represents $4.929$ ). Consider the sequence $\left( \{ k \log_{10}p \} \right)_{k \in \N}$ , where $\{ x \}$ denotes the fractional part of $x$ . Since the value $\log_{10}p$ is assumed to be irrational, then by the Equidistribution theorem , the sequence defined above is a dense subset of the interval $[0, 1]$ . Therefore, there exists $k_0 \in \N$ , such that $\{k_0 \log_{10}p\} \in \left[\log_{10} d_1.d_2 \ldots d_l, \log_{10}d_1.(d_2 \ldots d_l+1) \right)$ . It remains to show that the value $p^{k_0}$ has the desired property. Calculate: $p^{k_0} = 10^{k_0 \log_{10}p} = \underbrace{10^{\lfloor k_0 \log_{10}p \rfloor}}_{\text{is of the form } 10\ldots0}\cdot \underbrace{10^{\{k_0 \log_{10}p\}}}_{\in \left[d_1.d_2 \ldots d_l, d_1.d_2 \ldots d_l 9 \right)}$ , which shows the claim.

In order to solve the puzzle, we need to determine the natural numbers $p \geq 2$ such that $\log_{10} p$ is an irrational number. We will show the following: $\log_{10} p$ is a rational number if and only if $p$ is a (natural) power of 10. Suppose that $\log_{10}p = \frac{a}{b}$ , for some relatively prime integers $a$ and $b$ . W.l.o.g. we may assume, that $a > 0$ and $b > 0$ . We have that $10^{\frac{a}{b}} = p$ , hence $10^a = p^b$ and $2^a 5^a = p^b$ . Therefore $p = 2^r 5^s$ for some $r, s \in \N$ . We have that $2^{rb} 5^{sb} = 2^a5^a$ , thus $a = rb = sb$ , i.e. $r = s$ . Hence $p = 2^r 5^r = 10^r$ .

Therefore, all of the numbers $\log_{10} 2, \log_{10} 3, \ldots, \log_{10} 9$ are irrational and $\log_{10}10 = 1 \in \N$ .

As a side remark, I check how easy or hard it is to find the given number as a substring of a power of 2. On the graphic below, the point $(x, y)$ is highlighted if and only if $x$ is a substring of $2^y$ .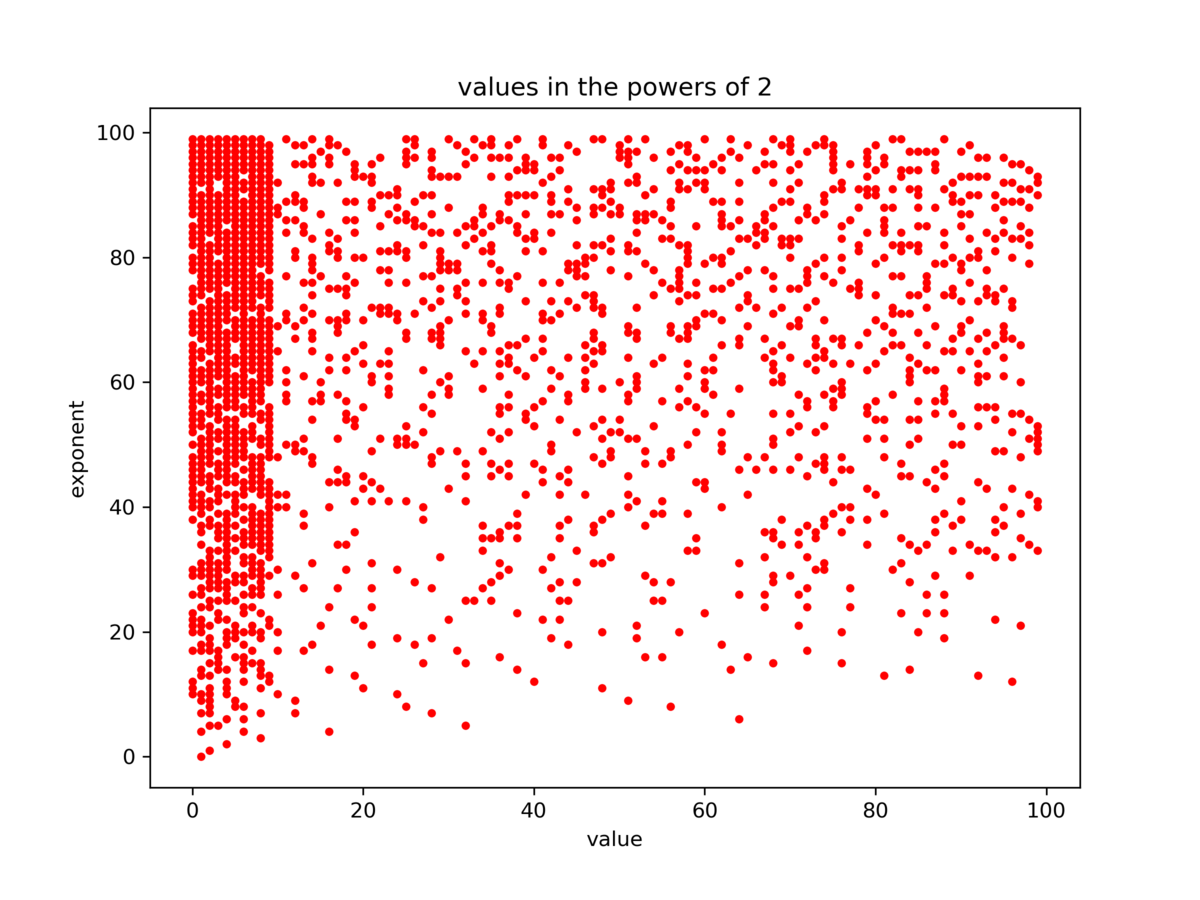

Feel free to use my python code for some further experiments. If you are looking for some more elaborated code, please have a look here .

Another explanation is to check the first 15 powers of 2:

$2^1 = 2$

$2^2 = 4$

$2^3 = 8$

$2^4 = 16$

$2^5 = 32$

$2^6 = 64$

$2^7 = 128$

$2^8 = 256$

$2^9 = 512$

$2^{10} = 1024$

$2^{11} = 2048$

$2^{12} = 4096$

$2^{13} = 8192$

$2^{14} = 16384$

$2^{15} = 32768$

After 15 powers, 10 is the only number that in these first 15 powers that is not a substring of these powers. Therefore, 10 is the answer. ( $2^{20} = 1048576$ , therefore 10 could be considered as a substring in $2^{20}$ .)