Subtraction and Division Look Similar
A − B = A ÷ B
If whole numbers A and B satisfy this equation, then what is A + B ?
Bonus: Can you explain why there is only one solution?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Great solution!
One note: you can simplify your factoring steps by directly noting that, for b = 1 , a b − b 2 = a ⇒ a ( b − 1 ) = b 2 ⇒ a = b − 1 b 2 = b + 1 + b − 1 1 .
We can first ask a more fundamental problem:
when does addition equal multiplication?
i.e. if B and C are positive integers such that B + C = B C , what are B and C ?
The solution to this question can be shown as follows.
Solution:
B C = B + C ⇒ ( B − 1 ) ( C − 1 ) = 1
Since B and C are both positive integers, B − 1 and C − 1 must divide 1.
Hence B − 1 = C − 1 = 1 and so B = C = 2 . []
[Now, as for the question posted by OP, I have the following solution.]
Solution:
Note that the whole numbers here mean non-negative integers.
B A must be an integer, for A − B is also an integer. Hence, B divides A .
Note that it is trivially true that A = 0 and B = 0 . Let A = B C for some positive integer C .
Putting A = B C into the given equation yields B C = B + C , which reduces to the "when does addition equal multiplication" problem.
By the previous solution, we have B = C = 2 and therefore A = B C = 4 .
Hence A + B = 6 is the required answer. []
ab - b² = a; ab - a = b²; a(b-1) = b²
(b-1) is a factor of b², possible only when b-1=1 Therefore, b=2, b²=a=4
So, a+b=6
But a=2 b=1 can also be another answer
We know that both A and B are integers. Then A-B is an integer, and therefore A/B is an integer. Since A/B is an integer, we know that B divides A. Then there exists an integer k such that Bk=A. Substituting Bk for A in our equation, we get Bk-B=Bk/B. Then Bk-B=k. We can factor this to obtain B(k-1)=k. Now note that k-1 is not 0. If it were, we would obtain the contradiction that B(0)=1. Then dividing by k-1, we get B=k/(k-1) and subsequently B=1+1/(k-1). Now, since both B and 1 are integers, we know that 1/(k-1) is an integer, which means that k-1 divides 1. Since the only divisors of 1 are 1 and -1, we know that either k-1=1 or k-1=-1. We can reject the latter since it will result in k=0 and B=0 (since B(k-1)=k would mean B(-1)=0), which is not possible since B divides A. Then k-1=1 and k=2. Then B(k-1)=k tells us that B=2, and since Bk=A, we know that A=Bk=2*2=4. Therefore A+B=4+2=6.
Your proof is right but a and b being integers do not mean a/b is an integer.
[Solution using pythagorean triplets] a − b = b a , where a , b ∈ Z + ⇒ a b − b 2 = a ⇒ b 2 − a b + a = 0 Take the discriminant of the quadratic: Δ = ( − a ) 2 − 4 ⋅ a ⇒ Δ = a 2 − 4 a ⇒ ( ∗ ) r 2 = a 2 − 4 a , for some r ∈ Z + ⇒ r 2 = a 2 − 2 ⋅ 2 ⋅ a + 4 − 4 ⇒ r 2 = ( a − 2 ) 2 − 4 ⇒ ( a − 2 ) 2 = r 2 + 2 2 Which means that ( ( a − 2 ) , r , 2 ) is a pythagorean triplet and for every pythagorean triplet A , B , C (where A 2 = B 2 + C 2 ) it true that ( A , B , C ) = ( k ( m 2 + n 2 ) , k ( m 2 − n 2 ) , k ⋅ 2 m n ) for some positive integers k , m , n . Now we have to consider two possible scenarios:
First scenario: 2 = k ⋅ 2 m n : ⇒ 1 = k m n ⟹ k , m , n ∈ Z + ( k = 1 and m = 1 and n = 1 ) ⇒ ( ( a − 2 ) , r , 2 ) = ( 2 , 0 , 2 ) ⇒ ( a , b ) = ( ( 2 + 2 ) , ( 2 a ± Δ ) ) ⟹ Δ = 0 ( a , b ) = ( 4 , 2 )
Second scenario: 2 = k ( m 2 − n 2 ) : ⇒ 2 = k ( m + n ) ( m − n ) ⟹ ( m + n ) ≥ ( m − n ) [ k = 1 and ( m + n ) = 2 and ( m − n ) = 1 ] Or [ k = 2 and ( m + n ) = 1 and ( m − n ) = 1 ] ⇒ [ k = 1 , m = 1 . 5 , n = 0 . 5 ] Or [ k = 2 , m = 1 , n = 0 ] But in the first case where ( k , m , n ) = ( 2 , 1 . 5 , 0 . 5 ) ∈ / Z + so we get no solution. In the second case where ( k , m , n ) = ( 2 , 1 , 0 ) we get: ( ( a − 2 ) , r , 2 ) = ( 2 , 0 , 2 ) ⇒ ( a , b ) = ( ( 2 + 2 ) , ( 2 a ± Δ ) ) ⟹ Δ = 0 ( a , b ) = ( 4 , 2 )
( ∗ ) : We expect the discriminant to be a perfect square of an integer so that b will have integer values.
b = 0 , a − b = a ÷ b ⇒ a b − b 2 = a ⇒ a b − b 2 − a + 1 = 1 ;
⇒ a ( b − 1 ) − ( b + 1 ) ( b − 1 ) = 1 ⇒ ( b − 1 ) ( a − b − 1 ) = 1 ;
a , b ∈ Z ⇒ { b − 1 = 1 ∧ a − b − 1 = 1 } ∨ { b − 1 = − 1 ∧ a − b − 1 = − 1 }
Which Gives us , b = 2 ∧ a = 4 ,
The second condition gives us , b = 0 , which is inappropriate!!!
□
4 - 2 = 4/2. therefore 4+2 = 6, A=4 & B = 2
A - B = A / B
A + B = (A / B) + B^{2}
A + B = A - B + B^{2}
B = - B + B^{2}
B^{2} - 2B = 0
B (B - 2) = 0
B = 0 V B = 2
A/B so B is not equal to 0, so B = 2
Then,
A - 2 = A / 2
2A - 4 = A
A = 4
So, A = 4 and B = 2
A + B = 4 + 2 = 6.
we see that b cannot be equal to 1 and also zero . further b-1 should divide b^2 which is only possible when b-1 divides -1 . as b cannot be zero it has to be two and a 4 which leads to their sum equal to 6
First, b = 0 . Next we have that a − b ∈ Z , so we have a = k b for some integer k. We rewrite k b − b = k , so b ( k − 1 ) = k , and b = k / ( k − 1 ) . The two integer solutions to this equation are clearly k = 0 and k = 2 , leading to b = 0 and b = 2 , and thus a = 0 and a = 4 . The only solution that satisfies b = 0 is { 2 , 4 } giving a sum of 6 .
A - B = A/B..... a whole number.
Dividing both sides by B,
(A/B) - 1 = A/B^2......a whole number.
Rearranging gives,
(A/B^2)(B - 1) = 1.
This is possible only if,
(A/B^2) = 1, and
B - 1 = 1,
so B = 2 and A = B^2 = 4.
A+B = 6.
6 is a perfect number too, that's creepy.
a-b = a/b => as a, b are integers therefore b | a => a = bk, k = some +ve integer. bk-b = k => b(k-1) = k as gcd(k-1, k) = 1, b|k and b is an integer => k can only be 2. so b = 2, a = bk = 4. => a+b = 6
A − B = B A ⟹ A ( B − 1 ) = B 2 ⟹ ( B − 1 ) ∣ B 2 ⟹ B = 2 .
So, A = 4 .
We have, A + B = 6 .
And why there is only one solution? Because, ( B − 1 ) ∣ B 2 ⟹ B = 2
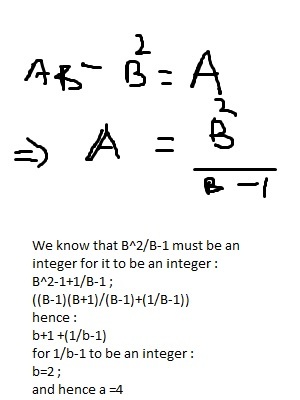
First, note that 4 − 2 = 4 ÷ 2 = 2 , so the answer is 4 + 2 = 6 . Let's see how to get that answer more methodically.
We multiply B for both sides, which gives a b − b 2 = a . This will be tricky to factorize, so I will add B for both sides of this equation. This gives a b − b 2 + b − a = b . Factorize the latter form gives a ( b − 1 ) − b ( b − 1 ) = b = ( a − b ) ( b − 1 ) Now wrote a in terms of b , which gives a = b − 1 b + b = b + ( 1 + b − 1 1 ) When you see the form a = b + 1 + b − 1 1 , no other whole number will make the fraction being whole number (as A must also be whole number) except -1 and 1 (division by zero is not allowed). Here, we will get b − 1 = ± 1 or b = 0 , 2 . Again, as the division by zero is not allowed, b = 0 , so b = 2 is the only solution, and when solving the equation, gives only ( a , b ) = ( 4 , 2 ) as the only answer, and a + b = 6