Such Triangle
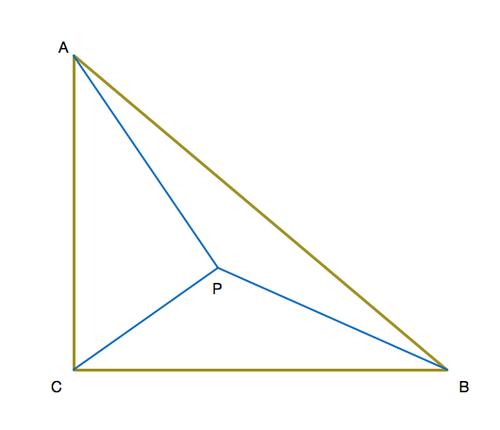 Isosceles triangle ABC has a right angle at C. Point P is somewhere inside ABC such that PA=11, PB=7, and PC=6. Legs AC and BC have length s=
a
+
b
2
. Find a+b.
Isosceles triangle ABC has a right angle at C. Point P is somewhere inside ABC such that PA=11, PB=7, and PC=6. Legs AC and BC have length s=
a
+
b
2
. Find a+b.
- This problem is taken from a reviewer given to me. I take no credit.
The answer is 127.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Sean Ty A little cleverer than your intended solution.
Log in to reply
Yep, well at least I learned something new today.
May I ask? How do you post a picture on a comment?
Log in to reply
LOL. My solution was a lot of vector bashing, using Mathematica to solve a nasty trig system of equations, and finally applying law of cosines. I think I spent about 6 hours on this ;pppp
Let B, A & P be (a,0), (0,a) & (x,y) resply. Then (a-x)^2+y^2=49, x^2+(y-a)^2=121, x^2+y^2=36 which can be solved simultaneously to obtain a=(85+42(2)^(1/2))^(1/2) or a+b =85 +42 =127
My solution was rotating the triangle 90 degrees counterclockwise about C, applying law of cosines several times. But I guess this works as well :) I won't be posting it because it needs a figure drawn for you to understand.
Just putting One Top 's solution in better way.
Let point C , A , B , P be ( 0 , 0 ) , ( 0 , a ) , ( a , 0 ) , ( x , y ) respectively.
Now we have following equations:
- x 2 + y 2 = 6 2
- ( x − a ) 2 + y 2 = 7 2
- x 2 + ( y − a ) 2 = 1 1 2
Starting with 2nd equation, x 2 − 2 a x + a 2 + y 2 = 4 9 ⇒ a 2 − 1 3 = 2 a x ⇒ x = 2 a a 2 − 1 3
Moving to 3rd equation, x 2 + y 2 − 2 a y + a 2 = 1 2 1 ⇒ a 2 − 8 5 = 2 a y ⇒ y = 2 a a 2 − 8 5
Substituting x and y in first equation,
4 a 2 ( a 2 − 1 3 ) 2 + ( a 2 − 8 5 ) 2 = 3 6
Bash bash bash
a 4 − 1 7 0 a 2 + 3 6 9 7 = 0 ⇒ a 2 = 8 5 ± 3 5 2 8 = 8 5 ± 4 2 2
8 5 + 4 2 = 1 2 7
Any idea why we ignored 8 5 − 4 2 2 ?
Log in to reply
Thanks Pranjal for putting my solution in a better way. In general, there are always two solutions possible to such problems. One corresponds to the point P inside the given triangle while the other is with the point P outside since √(85-42√2) would be a little over 5 units and that would mean that P is outside triangle ABC which is not the case as per the given diagram.
Rotate △ A B C about point C to get △ B B ′ C .
Point P is also mapped to point P ′ .
Connect P P ′ ; note that C P = C P ′ . Also, ∠ P C P ′ = 9 0 ∘
Thus, P P ′ = 6 2 + 6 2 = 6 2 .
Now, notice that △ B P P ′ is right, in particular, ∠ B P P ′ = 9 0 ∘ because ( 6 2 ) 2 + ( 7 ) 2 = ( 1 1 ) 2 .
Thus, ∠ B P C = 4 5 ∘ + 9 0 ∘ = 1 3 5 ∘ .
Now using LoC on △ B P C wrt ∠ B P C , we see that s 2 = 6 2 + 7 2 − 2 ⋅ 6 ⋅ 7 ⋅ cos 1 3 5 ∘ = 8 5 + 4 2 2 .
Thus, s = 8 5 + 4 2 2 and our answer is 8 5 + 4 2 = 1 2 7 .