Sudoku Hybrid
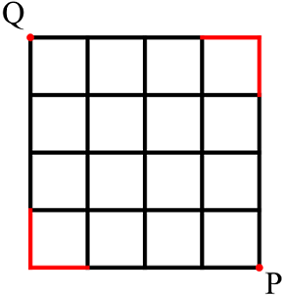
Brilli the Ant lives at the point P and wished to travel to the point Q , but because it's raining, the two other corners of the grid is inaccessible (so the ant can't move on the red lines).
If Brilliant can only 1 unit up or 1 unit to the left at a time, how many paths can Brilli take?
The answer is 68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Regardless of the path taken the ant will move a total of 4 times to the left and 4 times up and will take a total of 8 movements to reach the other corner. Label these movements 1, 2, 3, 4 ,5 ,6 ,7 and 8 in the order that the ant does them.
Now for each movement we are going to assign either ↑ or ← with a total of four of each arrow. Once we select in which movements (numbers) the ant moves to the left, the ones that it moves upwards are also defined. So we have ( 4 8 ) = 7 0 ways of doing this.
However there are 2 options that cannot happen (namely making the first four movements to the left or making the first four movements upwards). So the answer is 7 0 − 2 = 6 8