Points randomly chosen on a segment.

Probability Level 3

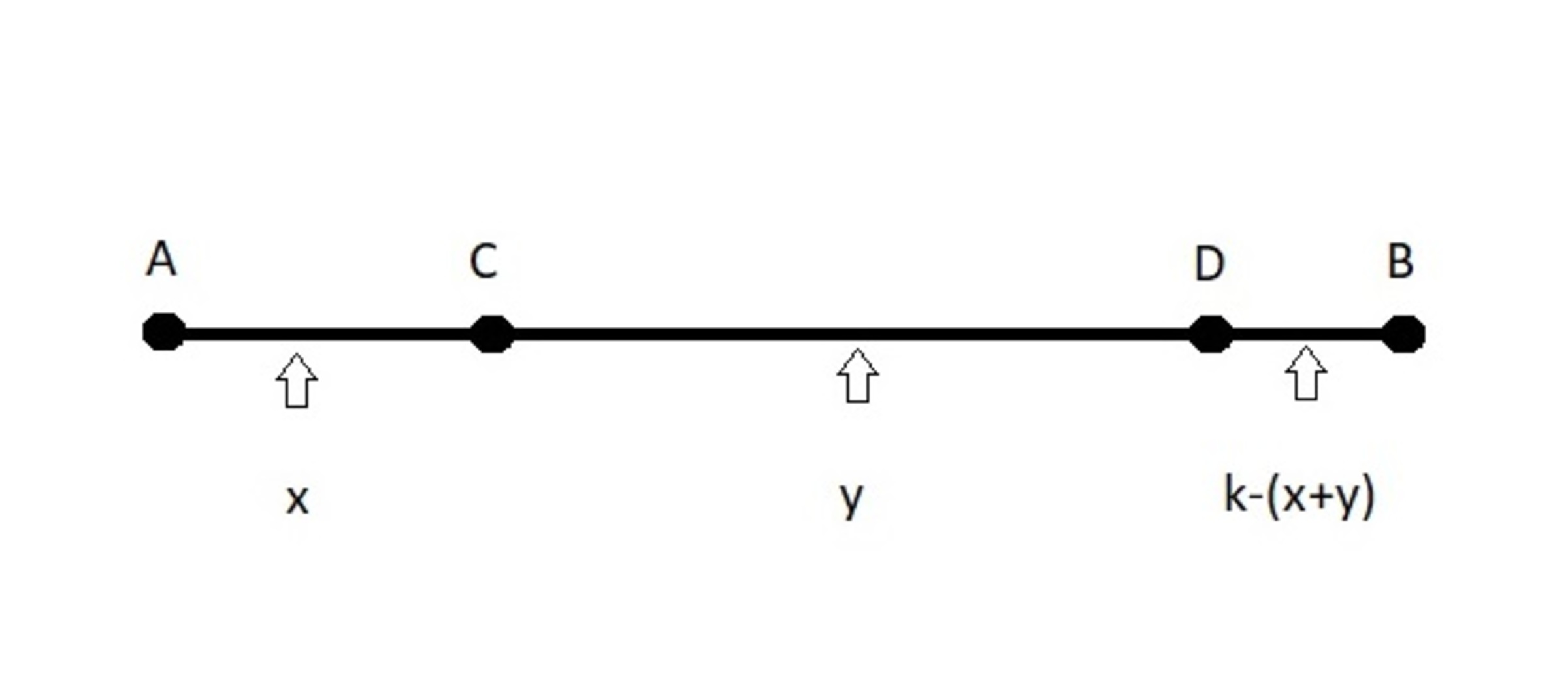
Let us consider a segment of A B AB of a given length k , k, where k k is an arbitrary positive number. We pick two points C C and D D on the segment randomly, so that they divide the given segment into three shorter segments of positive length. What is the probability that the three shorter segments can be used to form a triangle?

Note: This problem -that was suggested to me by my nephew Joey- is not intended to be original.


The answer is 0.25.

Arturo Presa by Arturo Presa , 62, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Arturo Presa
May 29, 2017

Let x x and y y be the length of two of the three shorter segments. Obviously, the regions of all possible pairs ( x , y ) (x, y) is P = { ( x , y ) ∣ x > 0 , y > 0 , x + y < k } . P=\{(x, y)| x>0, y>0, x+y<k\}. From the triangle inequality, we can get that the region of all pairs ( x , y ) , (x, y), such that the segments of length x , x, y , y, and k − x − y k-x-y can be used to form a triangle is E = { ( x , y ) ∣ x < k / 2 , y < k / 2 , x + y > k / 2 } . E=\{(x, y)| x<k/2, y<k/2, x+y>k/2\}. Then the probability that we are finding is p = a r e a ( E ) a r e a ( P ) = k 2 / 8 k 2 / 2 = 1 / 4 = 0.25 p=\frac{area(E)}{area(P)}=\frac{k^2/8}{k^2/2}=1/4=\boxed{0.25}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

I got stuck after triangle inequality. Nice problem

Peter van der Linden - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...