Sum
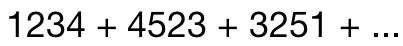
Find the sum of all 4-digit numbers formed by using the digits 1, 2, 3, 4, 5 and where no digit is to be repeated in any 4-digit number.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
There are 4 p 3 =24 ways we can have each digit in each spot if we always fix a digit. So (1111+2222+3333+4444+5555) * 24 = 399960
why (1111+2222+ .....)?
Log in to reply
The 1 comes 24 times in the units digit, 2 comes 24 times in the unit digits and it is true for all the digits and this is true for all the places(hundredths, ...). As the all digits in all places are coming same number of times, we can rearrange the digits as shown to calculate the final answer
(1+2+3+4+5)(24+240+2400+24000) = 399960
The number of ways of forming 4-digit numbers with no repeated digits is 5 P 4 = 1 2 0 . Let us consider the unit's place. In those 1 2 0 numbers, 1 , 2 , 3 , 4 , and 5 appear exactly the same number of times. Each digit appears 5 1 2 0 = 2 4 times. For the ten's place, hundred's place and thousand's place: 1 , 2 , 3 , 4 , and 5 appear equally the same number of times. Thus the sum of all those distinct 1 2 0 numbers is
1 0 0 0 ( 2 4 ) ( 1 + 2 + 3 + 4 + 5 ) + 1 0 0 ( 2 4 ) ( 1 + 2 + 3 + 4 + 5 ) + 1 0 ( 2 4 ) ( 1 + 2 + 3 + 4 + 5 ) + 1 ( 2 4 ) ( 1 + 2 + 3 + 4 + 5 ) = 3 9 9 9 6 0
Each digit appears 24 times at each decimal place, not 24 times in 120 times. Your solution is correct but your wording could confuse people.
Dus check:
Let's focus on all of the 4-digit numbers of which we know the rightmost number. For example, all four-digit numbers that end with a 4. How many of such numbers are there? Since we already have one digit in place (4, in the rightmost place), we can choose from 4 other digits (namely 1, 2, 3, and 5). Since we filled in one of the 4 places of the 4-digit number, we have three other places where we can put either a 1, 2, 3, or a 5. The number of four-digit numbers that end with a 4 is therefor 4 x 3 x 2 = 24.
But wait! We can put either 1, 2, 3, 4, or 5 in the rightmost place. For each of those the same thing applies; if we have 5 in the rightmost place, there will be 24 four-digit numbers with a 5 in the rightmost place.
Now, if we would add all four-digit numbers, think of adding them like this:
| 1 2 3 5 |
| 4 3 5 2 |
| 4 5 2 3 |
| 3 2 5 1 |
Let's focus on adding the one's place, i.e. adding the rightmost digits. We know that we have (24 * 1), and (24 * 2), and (24 * 3) etc. Factoring out the 24, we have 24 * (1 + 2 + 3 + 4 + 5) = 24 * 15.
Let's think about the hundreds place, the second digit from the right. Here, the same thing applies: if we'd know what number will be in that place, then for the other three places we can have 4 * 3 * 2 = 24 different four-digit numbers with a known number in the hundreds place. Again we'd have 24 * (1 + 2 + 3 + 4 + 5) = 24 * 15 BUT this time it's in the 10's place, so let's not forget to multiply with that as well: 24 * 15 * 10.
You can see where this is going with the hundreds place. Go get 'm tiger!
120 such numbers will be formed. This means each digit out of 1,2,3,4,5 is present 24 times in units, tens, hundreds, and thousands place. Sum of the digits is 1+2+3+4+5 = 15. Thus sum of the 120 numbers can be expressed as : 24 x 15 x (1000+100+10+1) = 399960
Notice 1234+5432=6666 this pattern continues ass you add the next smallest possible number and the next largest number. There are 120 different possible numbers divide that by 2 because we are adding 60 numbers and multiply that by 6666 which gives u the answer
There are ( 4 5 ) = 5 ways to choose the 4 numbers. There are 4 ! = 24 ways to rearrange the numbers. So there are 24*5 = 120 unique numbers.
The average of each unique number is 3333 since each of the 4 slots has the same average, ie. (1+2+3+4+5)/5 = 3.
Finally, the sum of all numbers is 120*3333 = 399960
Each digit will appear 4 ! = 2 4 times in each decimal position. Therefore we can factor it out in the sum. Now the units add up to 1 5 , the tens add up to ten times that and so on. So the final sum will be ( 4 ! ) ( 1 5 + 1 5 0 + 1 5 0 0 + 1 5 0 0 0 ) = 3 9 9 , 9 6 0
1 2 3 |
|
1 |
|
mathematica code
Total numbers formed using those 5 digits is 5P4. i.e. 120 numbers.
Since all digits will equally occupy the unit's place, therefore 1 will occur 24 times in unit's place. Similarly 2 will occur 24 times in unit's place. So on and so forth. Therefore sum of all digits in unit's place will be equal to 24 x (1+2+3+4+5)=24 x 15.
Similarly sum of all digits in ten's place will be equal to 24 x 150.
Therefore total sum of all numbers =24 x (15+150+1500+15000)=399960 .