There Are Some Interesting Cases To Consider
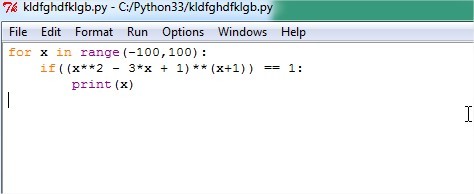
Find the sum of all integer solutions to the equation
( x 2 − 3 x + 1 ) x + 1 = 1 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
why not -1
Log in to reply
− 1 is only one of the four possible values for x . As noted in my solution, 0 , 1 and 3 are also valid solutions for x .
Nice idea!!
Log in to reply
wrong! any number to the power of 0 equals 1
Log in to reply
The exponent x + 1 equals 0 when x = − 1 , for which the base x 2 − 3 x + 1 = 5 . So while for any non-zero number y we have y 0 = 1 , (depending on the context we can consider 0 0 as being 0 , 1 or indeterminate), in this problem when the exponent equals 0 the base is necessarily 5 .
Yes. Nice idea.
Best Logical Thinking
@Brian Charlesworth what would be the no. Of solutions if x could take complex values?
( x 2 − 3 ⋅ x + 1 ) ( x + 1 ) = 1
ln ( x 2 − 3 ⋅ x + 1 ) ( x + 1 ) = ln ( 1 )
( x + 1 ) ⋅ ln ( x 2 − 3 ⋅ x + 1 ) = 0
ln ( x 2 − 3 ⋅ x + 1 ) = 0
e ln ( x 2 − 3 ⋅ x + 1 ) = e 0
x 2 − 3 ⋅ x + 1 = 1
x 2 − 3 ⋅ x = 0
x ⋅ ( x − 3 ) = 0
x = 0 ∣ x − 3 = 0
x = 0 ∣ x = 3
3 + 0 = 3
Going from step 3 to 4 implied division by (x+1). You need to show that x does not equal negative one before doing this.
Log in to reply
Furthermore, the use of logarithms restricts the domain to positive values. You would need to show that there exist no solutions for which the domain can be negative. This causes the loss of the solution x=1.
Log in to reply
In this case, the logarithm expression is ln(x^2-3x+1). Evaluated this expression at x=-1 yields ln((-1)^2-3(-1)+1) = ln(5), which is not a negative value. Therefore, x=-1 is in the domain of the function.
You miss the solutions x=1 and x=-1. Luckily for you that doesn't change the answer.
x=-1 is a solution you miss when you divide by x+1
fine method
LOL! Interesting approach.
If n^k = 1 then n = 1^(1/k). The only real solution is when n = 1. So x^2 - 3x + 1 = 1 or x^2 -3x = 0 so x = x = 0 or x = 3 summing to 3.
I simply factorized the quadratic equation and sum up the factors that were 1+2=3.
(x^2-3x+1)^ (x+1) = 1.
as 1^y =1 for any value of y,
(x^2-3x+1)^(x+1) = 1^(x+1)
=> x^2-3x+1 =1
=> x^2-3x = 0;
=> x = 0,3. :)
Guys I don't understand why we equating x^2 -3x +1 to -1
-1 to an even power equals +1
( x^2-3x+1 )^x+1 = 1 x^2-3x+1 = 1^(1/x+1) becose 1^anything=1 x^2-3x+1 = 1 x^2-3x = 0 x(x-3)=0 x=3,0 now putting the value of x in equation ( 9-9+1)^2= 1^2 =1 @ x=3 (0-0+1)^1= 1^1= 1 @ x=0
There are three options for which the given equation can be satisfied:
(i) the exponent x + 1 = 0 ⟹ x = − 1 , for which the base x 2 − 3 x + 1 = 5 = 0 ;
(ii) the base x 2 − 3 x + 1 = 1 ⟹ x ( x − 3 ) = 0 ⟹ x = 0 , 3 ;
(iii) the base x 2 − 3 x + 1 = − 1 ⟹ x 2 − 3 x + 2 = ( x − 1 ) ( x − 2 ) = 0 ⟹ x = 1 , 2 , and the exponent x + 1 is even. This is only the case for x = 1 .
Thus the given equation is satisfied for x = − 1 , 0 , 1 , 3 , the sum of which is 3 .