Sum of 3 random numbers < 1

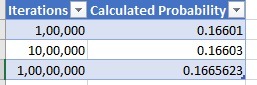
Call the three values $x,y,z$ . We can treat these as coordinates. The sample space is the unit cube with vertices $(0,0,0),(1,0,0),(0,1,0),(0,0,1),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$ , which has volume $1$ . The region we are interested in is the intersection of this cube with the region $x+y+z \le 1$ . This intersection is the tetrahedron with vertices $(0,0,0),(1,0,0),(0,1,0),(0,0,1)$ . The volume of this tetrahedron - which, since the sample space has volume $1$ , is also the required probability, is $\boxed{\frac{1}{6}}$ .

Theorm : The Probability of the sum of n random numbers less than or equal to s is (s^n)/n! where s is <=1 , hence the probability that the sum of 3 random numbers with values between (0,1) is 1/n! where n = 3 or is equal to 1/6.

Verified via Simulating the occurence of the event (r1+r2+r3 < 1) by generating a large number of random numbers. Here r1,r2 and r3 are random numbers

Sub randsum()

'rcount = 0

For i = 1 To 10000000

r1 = Rnd()

r2 = Rnd()

r3 = Rnd()

If (r1 + r2 + r3) < 1 Then

rcount = rcount + 1

End If

Next i

p = rcount / 10000000

MsgBox p

End Sub