Sum of all products

Relevant wiki: Sum of n, n², or n³

I will provide a geometric representation of the times table:

In the image above, the area of each rectangle represents a product. The red squares are the perfect squares. Notice that in this grid we have a big square with side length measuring $(1+2+3+4+...+y)$ .

The sum of the area of all rectangles (including the squares) will be the sum of all products in the times table. In this problem the sum is $44488900$ .

Hence, $(1+2+3+4+...+y)^2=90000\Rightarrow\ (1+2+3+4+...+y)=300$

Solving for $y$ :

$\displaystyle{1+2+3+4+...+y=\frac{(y+1)y}{2}=300}$

$\displaystyle{y^2+y-600=0}$

$\displaystyle{y=\frac{-1 \pm \sqrt{1^2-4\cdot 1 \cdot (-600)}}{2\cdot1}=\frac{-1 \pm \sqrt{2401}}{2}=\frac{-1 \pm 49}{2}}$

We only care for the positive solution for the equation which is $y=24$

Then the answer for this problem is $\boxed{24}$ .

Relevant wiki: Sum of n, n², or n³

$90\:000 = \sum_{a=1}^y \sum_{b=1}^y ab = \left( \sum_{a=1}^y a\right) \left( \sum_{b=1}^y b\right) = \left(\frac {y(y+1)} 2\right)^2.$ $\frac {y(y+1)} 2 = 300.$ "Completing the square" serves well here: $y(y+1) = y^2 + y = (y + \tfrac12)^2 - \tfrac14$ . $(y+\tfrac12)^2 = 600\tfrac14 = (24\tfrac12)^2.$ $y = \boxed{24}.$

Relevant wiki: Sum of n, n², or n³

The sum of product in the first line is $1+2+3+...+y = \frac{y(y+1)}{2}$ The sum of product in the $k$ -th line is $k+2k+3k+...+ky = k\frac{y(y+1)}{2}$ The sum of product of all lines is $\sum_{k=0}^{y} k+2k+3k+...+ky = \sum_{k=0}^{y} k\frac{y(y+1)}{2} = (\frac{y(y+1)}{2})^2 \Rightarrow (\frac{y(y+1)}{2})^2 = 90000\Rightarrow y^2+y-2\sqrt{90000} = 0 \Rightarrow y =\frac{-1+\sqrt{1+8\sqrt{90000}}}{2} = 24$

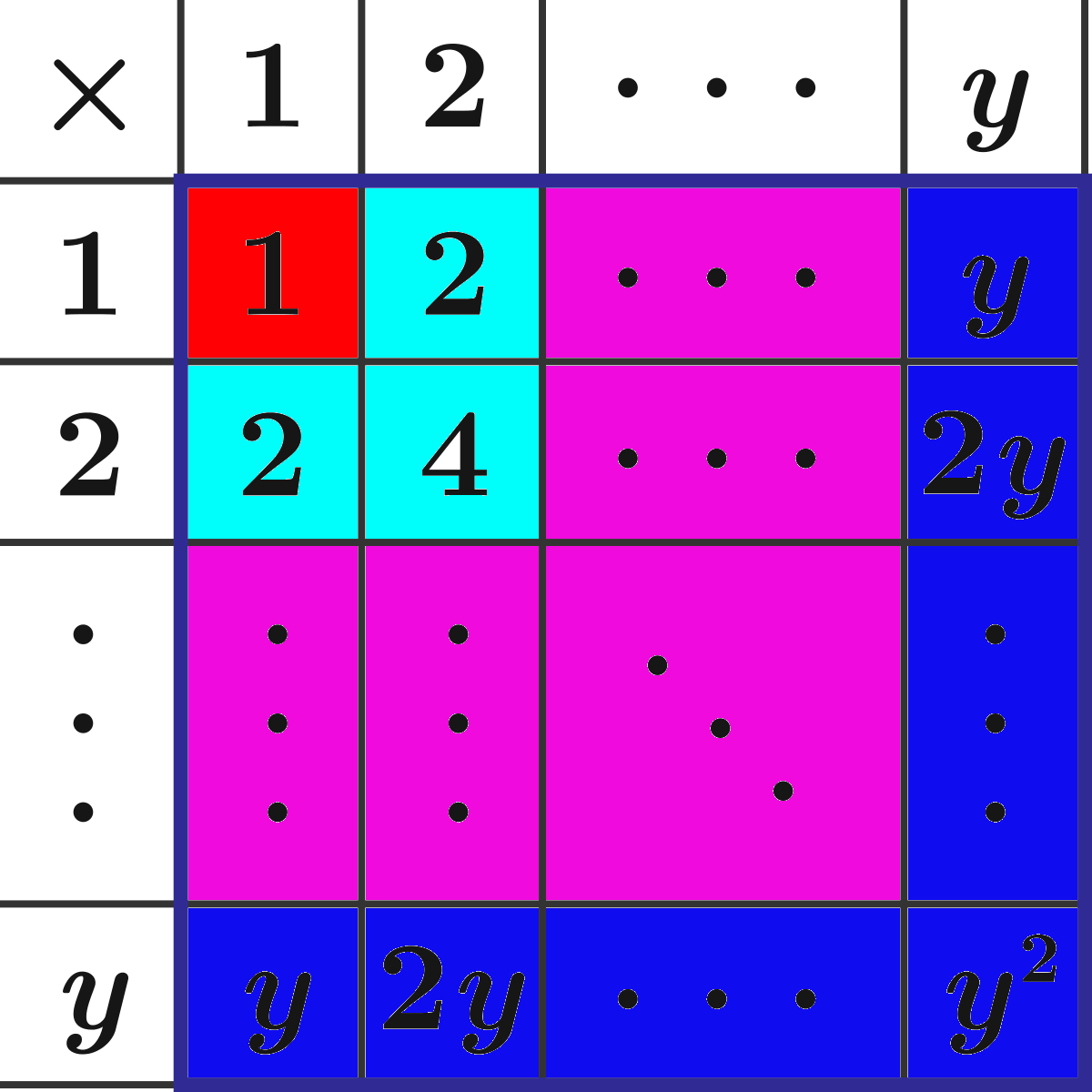Notice how the different colors for the values inside the box always sum to the cube of their multiplier (on the outside of the blue box). That means that the sum of the values inside the blue box unto a certain value y can be represented as $\sum_{n=1}^yn^3$ . When that value is equal to 90,000, the y value is 24. Hence the answer: 24

You can write the sum of products in a really nice manner: $S=(1\cdot 1+1\cdot 2+\cdots+1\cdot y)+(2\cdot 1+2\cdot 2+\cdots+2\cdot y)+\cdots+(y\cdot 1+y\cdot 2+\cdots+y\cdot y)$ Bringing the common factors to the front: $S=1(1+2+\cdots+y)+2(1+2+\cdots+y)+\cdots+y(1+2+\cdots+y)$ $S=(1+2+\cdots+y)(1+2+\cdots+y)=(1+2+\cdots+y)^2=\left(\frac{y(y+1)}{2}\right)^2$ But we know that $S=44488900$ and that $y$ should be positive, so $\frac{y(y+1)}{2}=\sqrt{90000}=300$ . Therefore: $1y^2+1y-600=0$ And all that we need to do it solve the quadratic equation and choose the positive value of $y$ : $y_{12}=\frac{-1\pm\sqrt{1+4\cdot 600}}{2}=\frac{-1\pm 49}{2}$ Hence, $y\in\{-25, 24\}$ , but $y>0$ , so the intended solution is 24 .

Simply, each side is $(1+2+3+...+y)$ so that the area is $(1+2+3+...+y)^2$ . We set this area equal to 90000. Thus, $(1+2+3+...+y)$ is $\sqrt{90000}$ = $300$ . Then, $(y+1)$ $\frac{y}{2}$ = $300$ . We multiply the terms on the left side, multiply both sides by $2$ , and subtract $600$ from both sides to get $y^2$ + $y$ - $600$ = $0$ . Factoring, we get $(y+25)$ $(y-24)$ and take the positive value 24 .

(1+2+…+y) (1+2+…+y)=90000.
1+2+…+y=sqrt(90000)
1+2+…+y=300.
(1+y)


y/2=300
(1+y)*y=600
y+y^2=600
y=24 or -25

What about a programming solution!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def main():
    n = 0
    i = 1
    while 1:
        n += i**2
        for j in range(i-1, 0, -1):
            n += 2*i*j
        if n == 90000:
            print('y equals to:', i)
            break
        i += 1

Which provides the answer: $\boxed{24}$

Each row or column is an AP

For $x^{th}$ row

$a = x$ , $l= xy$ and $n=y$ where a is first term, l is last term, n is number of terms

so sum of $x{th}$ row is

$\frac {y}{2} (x+xy)$

$=\frac {xy(y+1)}{2}$

and $x$ goes from $1$ to $y$

so total sum is

$\sum_{x=1}^y \frac {xy(y+1)}{2}$

$= \frac {y(y+1)}{2} \sum_{x=1}^y x$

$= \frac {y(y+1)}{2} \frac {y(y+1)}{2}$

$= \frac {y^2(y+1)^2}{4}$

When sum is 90000

$\frac {y^2(y+1)^2}{4} = 90000$ $y(y+1) = 600$

$\boxed{y=24 }$

Nothing to worry just add up the vertical columns one by one and u will get the sum of first y natural numbers. Then add them all up , solve a small quadratic i.e. y^2+y-600=0 then gives u y as 24

First I tried 2 random numbers Which of course didn't work After that I decide to try solving it wich was very funny so thank you for posting it I used the Sequences (not sure about the name) And the sum was like ((1+y)y/2)^2 Then trying to solving the equation ((1+y)y/2)^2=90000 (1+y)y-600=0 And the result will be y=24

Formula for sum of products in the square from number 1 to y is (n(n+1)/2)^2 e.g 1,9,36,100 So, 90000=(y(y+1)/2)^2 y(y+1)/2=300 y^2+y=600 y^2+y-600=0 (quadratic equation) Apply quadratic formula to solve for y. -(1)+sqrt 1^2-4(1)(-600)/2=24 Answer :24

I started out thinking 90000 is such a round number, so I thought maybe there is a pattern to the boxes as they get bigger. I started with 2x2 box which adds up to 9. 3x3 adds up to 36. 4x4 adds up to 100 !!!! Hang on this is a round number and they all happen to be squares. I did 6x6 which ends up being 441 which is 21^2. So the pattern of squares looks like.

1^2, 3^2, 6^2, 10^2, 15^2, 21^2... 1,3,6,10,15,21... are is the sequence of factorials 1!, 2!, 3!, 4!,5!, 6!...y!

thus (y!)^2=90000, y!=300 (square-root both sides)

(y/2)(y+1)=300 , y^2+y-600=0 (simplfied), (y-24)(y+25)=0

y equals 24 as -25 is not a possible blue box size.

Suppose £ means sigma Suppose we take 1 from the left column, we have to multiply it with every other number in the first row and add them. So it becomes 1(1+2+3+.......+y) = 1 £y Similarly taking 2 and multiplying it with every other number as adding, 2(1+2+3+....+y) =2 £y We have to do this for all numbers up till y. So end expression will be 1 £y + 2 £y + 3 £y +.......+y £y =£y(1+2+3+.......+y) =(£y)^2=90000 So £y=300 (y(y+1))/2=300 y(y+1)=600 Positive root is y=24

If you look at the pattern of 1^2, 2^2, 3^2, ... it turns out to be 1, 9, 36, 100. This pattern is (0+1)^2 = 1, (1+2)^2 = 9, (3+3)^2 = 36, (6+4)^2 = 100. The pattern is such that (x+y)^2 where x = the previous x+y, and y = the previous y +1. x follows this pattern: 0,1,3,6,10... and y follow this pattern: 1,2,3,4,5...

C++ solution
Int main()
{
Int a=1;
Int b=1;
Int c=1;
Int d=1;
Int w=0;
Int x=0;
Int z=0;
Int y;
Cin>>y;
While (b<y) { x=a+x;
a=a+1; b=b+1;}
While (c<y) { w=x*d; z=w+z;
d=d+1; c=c+1; }
Cout<<“num “<<z;
Return 0;
}
Then you insert 1 number higher than the number you are looking for, on this case, you insert 25 and here is your result, 24! You can do this with any number :)

I just thought about it and ran a bit of code. My math reasoning is lacking :-)

1
2
3
4
5
6
7

var sum = 0;
var up = 24;
for (var i = 1; i <= up; i++){
  for (var j = 1; j <= up; j++){
    sum = sum + (i*j);
  }
}

the online tool i used just printed sum in the end - hence no statement

Lazy person's brute force method.

Using this handsome lil' snippet of code I can easily make a multiplication table of any given size, and calculate the sum all of the numbers in it:

1
2
3
4
5
6
7

import numpy as np
y = 10
x = range(1,y+1)
table = np.array([[i*j for j in x] for i in x])
tableSum = table.sum()
print(table)
print('y = ', y, '\ttableSum =', tableSum)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

[[  1   2   3   4   5   6   7   8   9  10]
 [  2   4   6   8  10  12  14  16  18  20]
 [  3   6   9  12  15  18  21  24  27  30]
 [  4   8  12  16  20  24  28  32  36  40]
 [  5  10  15  20  25  30  35  40  45  50]
 [  6  12  18  24  30  36  42  48  54  60]
 [  7  14  21  28  35  42  49  56  63  70]
 [  8  16  24  32  40  48  56  64  72  80]
 [  9  18  27  36  45  54  63  72  81  90]
 [ 10  20  30  40  50  60  70  80  90 100]]
y =  10     tableSum = 3025 

So, all I need to do is turn my code into a loop that iterates through increasing values of y until I encounter a tableSum that's equal to (or bigger than) 90 000.

Oh, and since the table sum is the only important part, I'm not gonna keep showing the whole table every iteration. Okay, here's the loop version:

1
2
3
4
5
6
7

while tableSum < 90000:
    y += 1
    x = range(1,y+1)
    table = np.array([[i*j for j in x] for i in x])
    tableSum = table.sum()
    print('y = ', y, '\ttableSum =', tableSum)
print('The answer is: y =', y)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

y =  11     tableSum = 4356
y =  12     tableSum = 6084
y =  13     tableSum = 8281
y =  14     tableSum = 11025
y =  15     tableSum = 14400
y =  16     tableSum = 18496
y =  17     tableSum = 23409
y =  18     tableSum = 29241
y =  19     tableSum = 36100
y =  20     tableSum = 44100
y =  21     tableSum = 53361
y =  22     tableSum = 64009
y =  23     tableSum = 76176
y =  24     tableSum = 90000
The answer is: y = 24

$Q.E.D.$

Sum of y terms squared. Rearrange into a quadratic equation and then solve.

It's not elegant, but it works for me

Accumulate@Range[30]^2
this Mathematica code gives us the first 30 sums

{1,9,36,100,225,441,784,1296,2025,3025,4356,6084,8281,11025,14400,18496,23409,29241,36100,44100,53361,64009,76176,**90000**,105625,123201,142884,164836,189225,216225}

90000 is 24th on this list