Sum of Angles
What is the sum of the measures of the colored angles?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Lovely! I like that this solution uses nothing more then exterior angle theorem which we learn at the beginning of geometry course. Thank you.
The figure can be divided into one pentagon and five lateral triangles. The five triangles include the exterior angles of the pentagon twice. The sum of the angles of the five triangles 1 8 0 ° × 5 = 9 0 0 ° . The exterior angles of the pentagon = 3 6 0 ° . So, the required angles = 9 0 0 ° − 3 6 0 ° × 2 = 1 8 0 ° .
Moderator note:
The process of taking a polygon and extending the sides until they meet at points on the outside is called stellation . A first-order stellation stops extending after the first intersection.
The process given in this answer can be used to find the sum of the measures of corner vertices of any first-order stellation. Specifically, given n sides, the triangles have a sum of 1 8 0 ∘ × n and the external angles not part of the corner vertices sum to 3 6 0 ∘ × 2 = 7 2 0 ∘ . So the general formula for the sum of the measures of corner vertices is 1 8 0 ∘ × n − 7 2 0 ∘ .
Exactly my thinking! (+1)
Solution 1:
We will use that in a triangle the sum of any two angle is equal to the third angle's exterior angle, and that in a triangle the sum of the angles equals to
1
8
0
°
.

Then β + ϵ = ∠ B F A and γ + ω = ∠ E G A .
So α + β + γ + ϵ + ω = ∠ F G A + ∠ F A G + ∠ A F G = 1 8 0 °
Solution 2:
We wil use that in a pentagon the sum of the angles is ( 5 − 2 ) ∗ 1 8 0 ° = 5 4 0 ° , (and that in a triangle the sum of the angles is equal to 1 8 0 ° ).

If
-
N ° = α + β + γ + ϵ + ω
-
K ° equals to the sum of the red angles
then 5 4 0 ° − K ° = N ° .
The red angles are in five triangles, so if the sum of the yellow, green, light blue, dark blue and pink angles is M ° , then 5 ∗ 1 8 0 ° − M ° = K ° .
However we know that M ° is 5 4 0 ° , because there is a smaller pentagon inside with the yellow, green, light blue, dark blue and pink angles.
So K ° = 9 0 0 ° − 5 4 0 ° = 3 6 0 ° , and
α + β + γ + ϵ + ω = 5 4 0 ° − 3 6 0 ° = 1 8 0 °
Your second solution is cool
2 9 0 0 − 5 4 0 = 1 8 0

Why it is divided by 2?
Log in to reply
Each angle (except for the angles in the pentagon) has been used twice by identifying the 5 composite triangles - hence each point of the pentagram in the gif counting up to 2 (and the need to divide by 2).
Thanks @jonathan
Nice GiF! I'm always curious to learn: How did you create GIFs? Is there a special app for this? Most sites I go to (to create Gifs) are not particularly user friendly.
Log in to reply
Thanks! I create a series of images, and upload them to https://giphy.com/create/slideshow
It's the first site I found that doesn't watermark the GIFs. But, in my experience, a composition of over about 20 images will start to cause errors with the GIFs made there.
On the assumption that the question has a single solution independent of the regularity of the star - or lack thereof - we might as well just solve it for the easy case where the interior pentagon is regular. In that pentagon, angles are 5 5 4 0 = 1 0 8 ∘ . That would make the base angles of any of the outer isosceles triangles 7 2 ∘ , so the outer angles would be 1 8 0 − 2 × 7 2 = 3 6 ∘ . Five of those sum to 1 8 0 ∘ .
Obviously, this doesn't suffice as a demonstration of the general result, but since this question was posed in a way that implies there's only one general solution, it gets the job done.
Trace the star. At each of n = 5 points with angle α i we turn over an angle of 1 8 0 ∘ − α i . It is also clear that we turn r = 2 full revolutions while doing this. Thus i = 1 ∑ n ( 1 8 0 ∘ − α i ) = r ⋅ 3 6 0 ∘ , i = 1 ∑ n α i = ( n − 2 r ) ⋅ 1 8 0 ∘ , i = 1 ∑ 5 α i = ( 5 − 4 ) ⋅ 1 8 0 ∘ = 1 8 0 ∘ .
This is the approach I used. It's similar to one way to generate the sum of the interior angles of a convex pentagon (one starts by noticing that the sum of the exterior angles is 360 degrees).
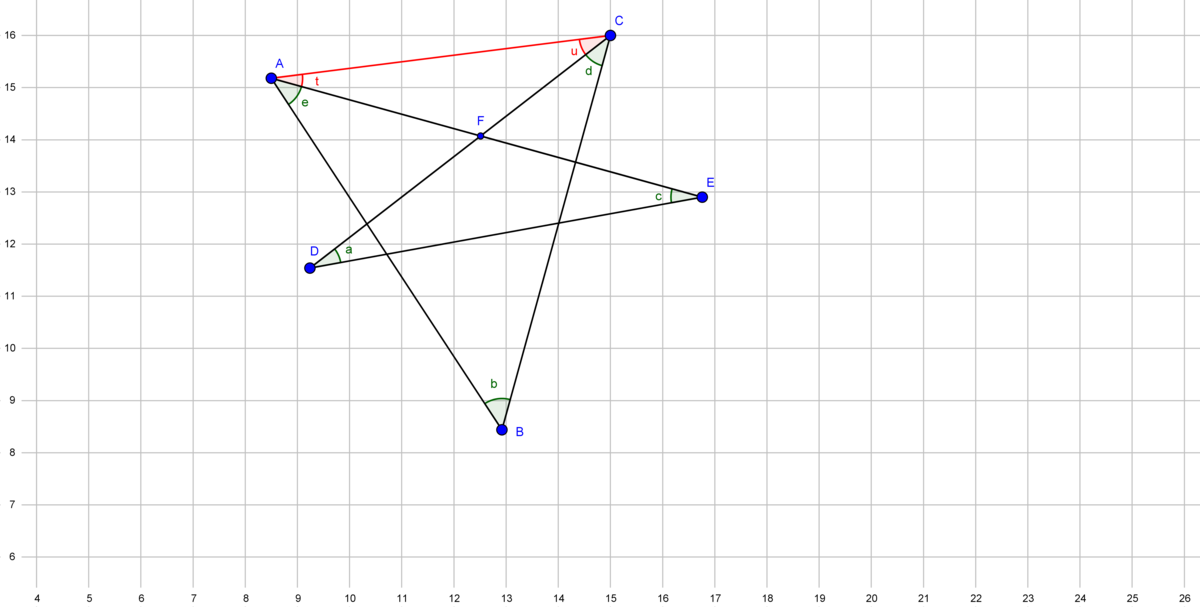 First, draw a line segment
A
C
(the red one)
Notice in triangle
A
B
C
, we have
t
+
u
+
e
+
d
+
b
=
1
8
0
.
Then notice triangles
A
F
C
and
D
F
E
. They share an angle
∠
A
F
C
=
∠
D
F
E
. So the sum of the other two angles in each triangle must be equal. Which means that
t
+
u
=
a
+
c
. And
a
+
b
+
c
+
d
+
e
=
1
8
0
.
First, draw a line segment
A
C
(the red one)
Notice in triangle
A
B
C
, we have
t
+
u
+
e
+
d
+
b
=
1
8
0
.
Then notice triangles
A
F
C
and
D
F
E
. They share an angle
∠
A
F
C
=
∠
D
F
E
. So the sum of the other two angles in each triangle must be equal. Which means that
t
+
u
=
a
+
c
. And
a
+
b
+
c
+
d
+
e
=
1
8
0
.
If you took the two bottom points and the top point and stretched the star to be tall and thin, the angle of those three points would approach zero, while the angle of the left and right points would approach 90 degrees, making the answer 180 degrees.
The total of the five angles will remain the same if the figure is fully symmetrical, so we can simply realise that a pentagon's sum of inner angles adds up to 540 degrees (each corner after 3 adds 180 degrees to the total) and then get the angles next to them, which will make two 72 degree angles along with the tips, which means that for a symmetrical figure, all of the tips are (180-72 2) = 32 degrees, so 5 32 = 180 degrees.
Quick headcount solution: you take the triangles formed by two of the opposing marked angles and an angle in the inner pentagram. There are 5 of these, which adds up to 5 * 180. The pentagram has a total of 180 * (5 - 2) = 3 * 180. The marked angles were used two times, while the angles of the pentagram only once, so the sum of the marked angles is (5 * 180 - 3 * 180) / 2 = 2 * 180 / 2 = 180
My quick and lazy answer:

We have 5 of these triangles. The colored angle on each is 1 8 0 ∘ − ( t h e g r e e n a n g l e + t h e r e d a n g l e ) .
The sum of all the green angles (going around the whole pentagon) is 360^\circ. Same for the red.
So we have 5 × 1 8 0 ∘ − 3 6 0 ∘ − 3 6 0 ∘ . Or, as I like to call it because I hate arithmetic, 5 × 1 8 0 ∘ − 4 × 1 8 0 ∘ = 1 8 0 ∘
The internal angles of a regular pentagon are 108 Deg totalling 540 Deg. 540 - 360 = 180 Deg

We can set up following equations:
m = 1 8 0 ∘ − a − b
n = 1 8 0 ∘ − b − c
p = 1 8 0 ∘ − c − d
q = 1 8 0 ∘ − d − e
r = 1 8 0 ∘ − e − a
Summing:
∑ = m + n + p + q + r = 5 × 1 8 0 ∘ − 2 ( a + b + c + d + e )
Notice that a , b , c , d , e are all external angles of internal pentagon and their sum is 3 6 0 ∘ (in fact, sum of external angles of any polygon is 3 6 0 ∘ ).
Hence, ∑ = m + n + p + q + r = 5 × 1 8 0 ∘ − 2 × 3 6 0 ∘ = 1 8 0 ∘ .
Going around the pentagon clockwise - it has a set of external angles = 360. Go around the pentagon anticlockwise and there are another set of external angles = 360. These 2 groups of angles make 2 of the 3 angles in each of the five triangles (call these the "base" angles).
However 5 triangles have 5x180 degrees (or more usefully here, 2.5x360 degrees). So if the 2 "base" angles are taken away, it leaves the coloured angles adding up to 0.5x360 degrees --> 180 degrees.
I found a slick way to solve this really easily...
If we assume that the sum of the five angles is constant (which must be true for one of the given answers to be correct), then do the following:
If the sum of the five angles is constant, then we can manipulate the figure by moving the five marked points any way we want (while preserving the shape) and the sum of the angles should stay the same. Take the bottom two points (dk blue and purple) and move them together so they coincide. This makes the red angle zero, and what we have left is a triangle with a line in the middle (the dk blue angle and the purple angle combine to make a single angle and the red angle is gone). The sum of the angles in a triangle is 180 degrees, so that's the answer.
Notes:
1) If you argue that by making two points coincide, you've changed the type of figure you're dealing with, note that this is a well-posed problem and that you could make the two points arbitrarily close to one another - for simplicity of exposition, I ignored this detail.
2) I admit that this only works if you've been told (or assume) that the sum of the angles is constant. This argument does not prove that the sum is constant - for example, at first glance, it could be true that the sum just approaches 180 as any two points approach each other, but it could be different from 180 in general.
But why can we assume that the sum of the 5 angles is constant? How do you know that this sum might not vary?
Let 1 , 2 , 3 , 4 and 5 be the angles of the irregular pentagram .
By the Exterior Angle Theorem , ∠ F G D = 1 + 3 because ∠ 1 and ∠ 3 are remote angles. It follows that ∠ G F D = 2 + 4 since it is an exterior angle with remote angles 2 and 4 . The sum of the interior angles of △ F G D = 1 + 3 + 2 + 4 + 5 = 1 8 0 ∘ . But these are the angles of the pentagram. Hence, the sum of the angles of the pentagram is 1 8 0 ∘ .