Sum of areas of squares
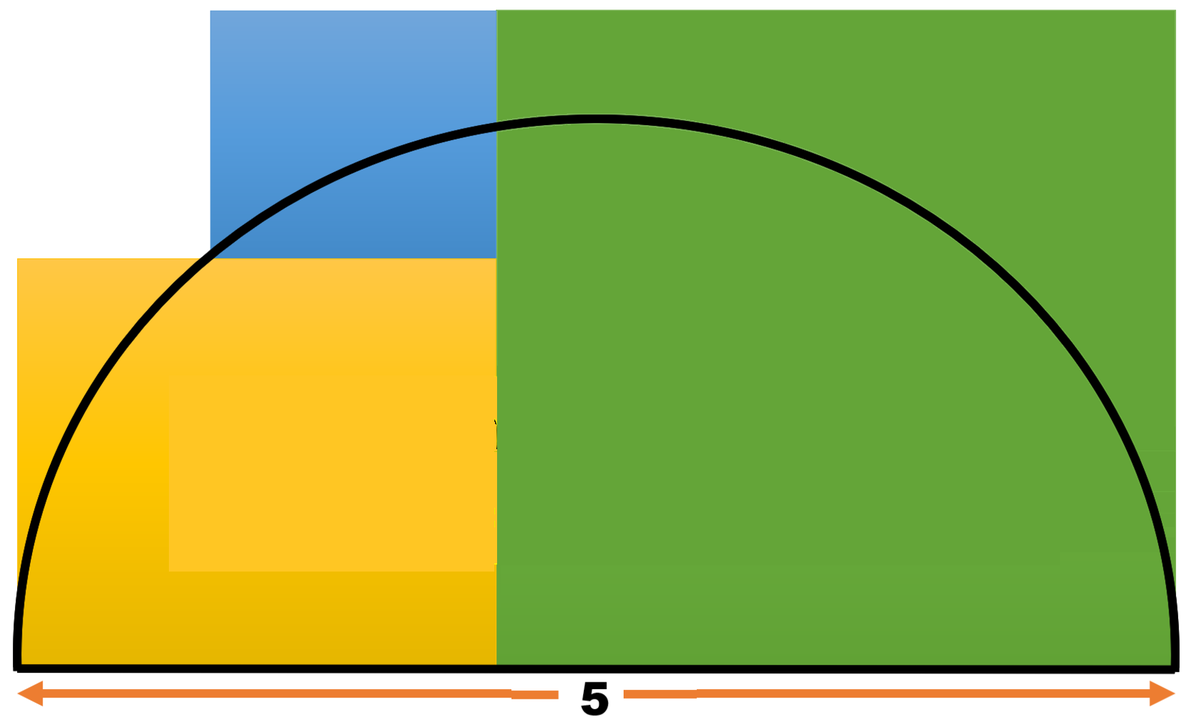
Three squares each has a vertex on a semicircle with a diameter of 5 . Find the sum of areas of the three squares.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
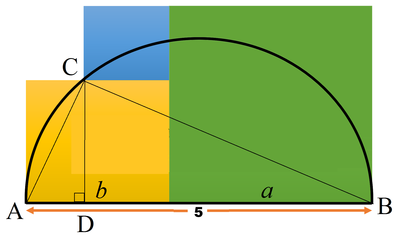
Let the side length of the green square be a and that of the yellow square be b , where a > b . Then the side length of the blue square is a − b and the diameter A B = a + b = 5 . Let C be the vertex of the blue square on the semicircle and C D be perpendicular to A B . Because A B is a diameter, ∠ A C B = 9 0 ∘ . Therefore △ A B C and △ B C D are similar. Then we have:
A B B C B C 2 C D 2 + B D 2 b 2 + ( a + a − b ) 2 4 a 2 − 4 a b + 2 b 2 2 a 2 − 5 a b + 3 b 2 ( 2 a − 3 b ) ( a − b ) ⟹ 2 a = B C B D = A B ⋅ B D = A B ⋅ B D = ( a + b ) ( a + a − b ) = 2 a 2 + a b − b 2 = 0 = 0 = 3 b Since a > b
Since a + b = 5 , ⟹ a = 3 , b = 2 , and a − b = 1 , and the sum of areas of the three squares is a 2 + b 2 + ( a − b ) 2 = 9 + 4 + 1 = 1 4 .
Why not 1 2 . 5 ? In that case the blue and the yellow squares will merge into one square.
Excuse me, how can these two squares merge into one square? I don't see how that's possible.
They don't exactly "merge into one" in this case - the side of the blue square is zero (the yellow and green squares both have side 2 5 ).
See @Bill Chapp 's solution which explains this case too. In @Chew-Seong Cheong 's solution, it's the discarded case where a = b .
Let x be the distance from the center of the semi circle to the right edge of the yellow square. The yellow square has side length r − x , the green square has side length r + x , and the blue square has side length ( r + x ) − ( r − x ) = 2 x . The sum of the areas of the squares is then A = ( r − x ) 2 + ( r + x ) 2 + ( 2 x ) 2 = 2 r 2 + 6 x 2 .
Draw the radius of the semicircle to the vertex of the blue square on the semicircle, then the perpendicular down to the diameter of the semicircle. The right triangle formed has height r − x , base x + 2 x = 3 x , and hypotenuse r . By the Pythagorean Theorem: ( r − x ) 2 + ( 3 x ) 2 = r 2 ⇒ x = 5 r or x = 0 .
x > 0 ⇒ x = 5 r = 2 1 . The sum of the areas is A = 2 ⋅ ( 2 5 ) 2 + 6 ⋅ ( 2 1 ) 2 = 1 4 .
(Note that x = 0 corresponds to the blue square disappearing, and the yellow and green squares each having side length 2 5 . In this case, the total area is A = 1 2 2 1 ).