SUM OF CUBES OF THE SIDES!!
Level
pending
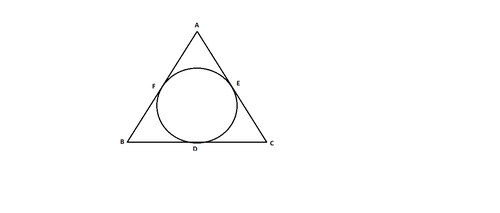In a triangle ABC, the incircle touches the sides BC, CA and AB at D, E ,F respectively . If radius of incircle is 4 unit and BD , CE and AF be consecutive natural numbers , then the sum of cubes of the length of sides must be
The answer is 8316.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
given figure
Let BD, CD and AF be of lengths n-1, n , n+1 respectively .
since, the lengths of the tangent, from an external point to the circle are equal.
Then BF=BD=n-1,CD=CE=n and AE=AF=n+1
BC=2n-1,CA=2n+1,AB=2n
thus,
s=3n
NOW,
tanC/2=r/n tanB/2=r/(n-1)
so that tan(B/2+C/2)=(r/n-1+r/n)/(1-r²/n(n-1))
cotA/2=(2rn-r)/n²-n-r² since cotA/2=n+1/r
n³-3r²n-n=0
n³-48n-n=0
we get
n=0 or n=7
so the sides of the triangle are 13,14,15 units and required sum is 13³ + 14³ +15³= 8316