Sum of factorials

Number Theory Level 2

$\left( \sum_{I=1}^{100} I!\right) \bmod {100} = \, ?$

Notation : $!$ denotes the factorial notation. For example, $8! = 1\times2\times3\times\cdots\times8$ .

13 10 11 12

2 solutions

Zee Ell
Aug 6, 2016

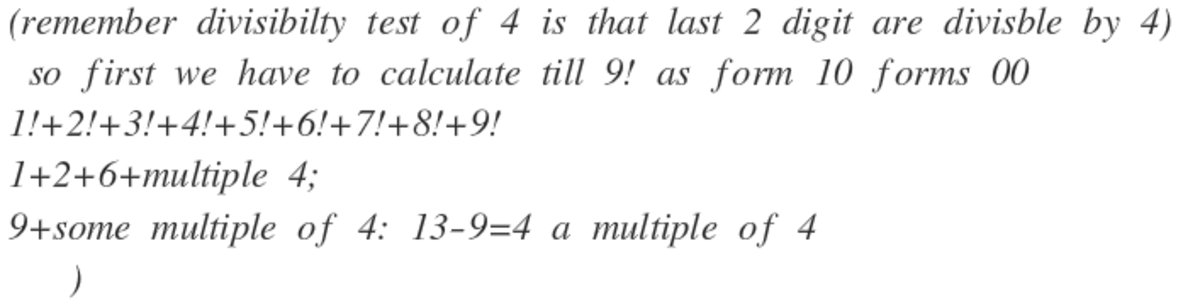
As $100 = 2^2 × 5^2$ , the first factorial (and since factorials of bigger numbers are multiples of factorials of all smaller integers, all subsequent factorials will have a 0 remainder by 100) , which is divisible by 100 is 10!

Therefore, it is enough to add the last two digits of the factorials of the integers from 1 to 9:

1+2+6+24+20+20+40+20+80 = 213, which means, that our answer should be:

213 mod 100 = $\boxed {13}$

Simrat Singh
Aug 10, 2016

Sum of factorials

2 solutions

0 pending reports