Sum of First 24 Terms
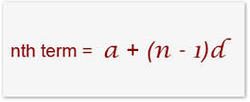 Find the sum of first 24 terms of the A.P.
a
1
,
a
2
,
a
3
,
a
4
,
…
if it is known that
a
1
+
a
5
+
a
1
0
+
a
1
5
+
a
2
0
+
a
2
4
= 225.
Find the sum of first 24 terms of the A.P.
a
1
,
a
2
,
a
3
,
a
4
,
…
if it is known that
a
1
+
a
5
+
a
1
0
+
a
1
5
+
a
2
0
+
a
2
4
= 225.
The answer is 900.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
we know that terms in AP are a,a+d,a+2d.....so on then sum of first 24 terms is equal to a+a+d+a+2d+......+a+23d, which is equal to 24a+276d....., Given that a1+a5+a10+a15+a20+a24=225, which is simplified to 6a+69d=225, hence 4*(6a+69d)=24a+276d=900
a {1} = a & a {5} = a +4d & a {10} = a +9d & a {15} = a +14d & a {20} = a +19d & a {24} = a +23d
Given, a {1} + a {5} + a {10} + a {15} + a {20} + a {24} = 225 => a + a +4d + a +9d + a +14d + a +19d + a +23d = 225 => 6a + 69d = 225 => 3 (2a + 23d) = 225 So, 2a + 23d = 75
Now, S_{24} = \frac{24}{2} (2a + 23d) = 12 \times 75 = \boxed{900}
a₁ + a₅ + a₁₀ + a₁₅ + a₂₀ + a₂₄ = 225 => a + [a+(5−1)d] + [a+(10−1)d] + [a+(15−1)d] + [a+(20−1)d] + [a+(24−1)d] = 225 => a + (a + 4d) + (a + 9d) + (a + 14d) + (a + 19d) + (a + 23d) = 225 => 6a + 69d = 225 => 2a + 23d = 75 Now, a₁ + a₂ + a₃ + a₄ + a₅ + .... + a₂₄ = (½) x [a₁ + a₂₄] x 24 = (½) x [a + a +(24−1)d] x 24 = (½) x [a + a + 23d] x 24 = (½) x [2a + 23d] x 24 = (½) x 75 x 24 = 900
Looking on the sum of a1,a5,a10,a15,a20 and a24:
Sn = (n/2)(a1+an)
Using Sn = 225 and n =6,
we will get (a1+an) = 75
Using (a1 + an ) to compute for the sum of the first 24 terms with n=24
Sn = (n/2)(a1 + an)
Sn = (24/2)(75)
Sn = 900
an = a1 + (n-1)d & Sn = n/2 (2a1+(n-1)d) or n/2(a1+an) or (an+a1)(an-a1)/(a2-a1) for n=24 we find d=1 so S = 12(a24+a1) now a1+a5+a10+a15+a20+a24 = 225 or a1+a1+4+a1+9+a1+14+a1+19+a1+23=225 a1 = 26 & a24 = 49 S24 = 12(26+49) =900
Hello,
Given that a(1) + a(5) + a(10) + a(15) + a(20) + a(24) = 225
a + (a+4d) + (a+9d) + (a+14d) + (a+19d) + (a+23d) = 225
6a + 69d = 225
2a + 23d = 75
2a = 75 - 23d (1),
for sum of the 1st 24 terms,
S(24) = 12(2a + 23d),take (1) substitute into this S(24),
= 12(75 -23d + 23d)
=12(75)=900
therefore S(24) = 900,
thanks....
S 2 4 = 2 2 4 ( 2 a 1 + 2 3 d ) , where a 1 is the first term and d is the common difference.
S 2 4 = 24 a 1 + 276d.
Now, 225 = a 1 + a 5 + a 1 0 + a 1 5 + a 2 0 + a 2 4
225 = 6 a 1 + 6 9 d
We can see that, 24 a 1 + 276d = 4 × ( 6 a 1 + 6 9 d )
So, S 2 4 = 4 × 2 2 5 = 9 0 0