Sum Of Fourth Powers?
n → ∞ lim 1 4 + 2 4 + ⋯ + n 4 n 5 = ?
Bonus : Generalize this.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Greattttt
Challenge Master Note : Now solve this question without using Riemann Sums.
Log in to reply
Then we can use : r = 1 ∑ n r 4 = 3 0 n ( n + 1 ) ( 2 n + 1 ) ( 3 n 2 + 3 n − 1 )
Log in to reply
Second Challenge Master Note : This time, solve this question without using Riemann Sums nor the closed form for r = 1 ∑ n r 4 .
We note that n → ∞ lim 1 m + 2 m + 3 m + . . . + n m n m + 1 = b n a n is such that 0 < b 1 < b 2 < . . . < b n < . . . and lim n → ∞ b n = ∞ is a ∞ / ∞ case and we can apply Stolz–Cesàro theorem as follows:
L = n → ∞ lim 1 m + 2 m + 3 m + . . . + n m n m + 1 = n → ∞ lim b n + 1 − b n a n + 1 − a n = n → ∞ lim ∑ k = 1 n + 1 k m − ∑ k = 1 n k m ( n + 1 ) m + 1 − n m + 1 = n → ∞ lim ( n + 1 ) m ( n m + 1 + ( m + 1 ) n m + 2 ( m + 1 ) m n m − 1 + . . . + 1 ) − n m + 1 = n → ∞ lim n m + m n m − 1 + 2 m ( m − 1 ) n m − 2 + . . . + 1 ( m + 1 ) n m + 2 ( m + 1 ) m n m − 1 + 2 ( m + 1 ) m ( m − 1 ) n m − 2 + . . . + 1 = n → ∞ lim 1 + m n − 1 + 2 m ( m − 1 ) n − 2 + . . . + n − m ( m + 1 ) + 2 ( m + 1 ) m n − 1 + 2 ( m + 1 ) m ( m − 1 ) n − 2 + . . . + n − m = m + 1 By binomial expansion Divide up and down by n m
For m = 4 , the answer is m + 1 = 5 .
Great. Another approach is to show that 1 m + 2 m + 3 m + ⋯ + n m = m + 1 1 n m + 1 + O ( n m ) .
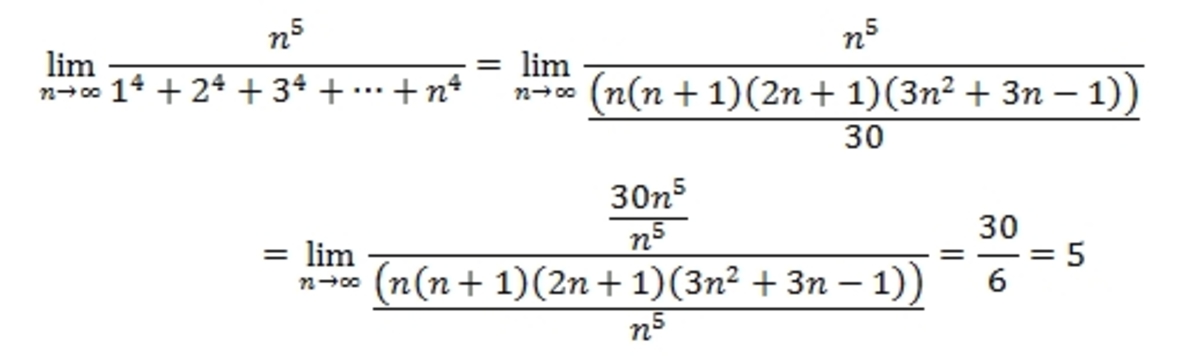
Relevant wiki: Riemann Sums
See Reimann Sums U = n → ∞ lim r = 1 ∑ n r p 1 p + 2 p + 3 p ⋅ + n p n p + 1
= n → ∞ lim n 1 r = 1 ∑ n ( n r ) p 1 = ∫ 0 1 x p d x 1 = p + 1
For this question ,put p = 4 , so that:-
n → ∞ lim 1 4 + 2 4 + ⋯ + n 4 n 5 = 5