Sum of Neighbouring Cells
Each cell in a grid contains one of the digits and
Based on this original grid, a new grid--shown below--is formed, in which the number in each cell represents the sum of the digits in the neighboring cells in the original grid, i.e. all the cells that surround a given cell horizontally, vertically, and diagonally.
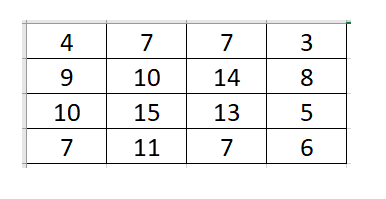
Determine the number of 2's in the original grid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 1 6 simultaneous linear equations to solve for the grid entries. This set of equations is consistent, and the associated 1 6 × 1 6 matrix has rank 1 4 , so there is a 2 -parameter family of solutions as follows: a a − b 2 + a − b 1 + a b 4 − a 3 − a 2 + b b + 2 1 − a 2 − a 3 + b a + 2 a − b 1 + a − b a − 1 The facts that 1 − a , a − 1 and 3 + b are integers between 0 and 3 tell us that a = 1 and b = 0 , making the grid 1 1 3 2 0 3 2 2 2 0 1 3 3 1 2 0 and hence there are 5 2 s in the grid.