Sum of sines

Think about it graphically. It is clear that $\sin90$ is the greatest possible value. However, $3\times 90 = 270$ , not $360$ as required. Therefore, we need some of the values to be shifted to the right.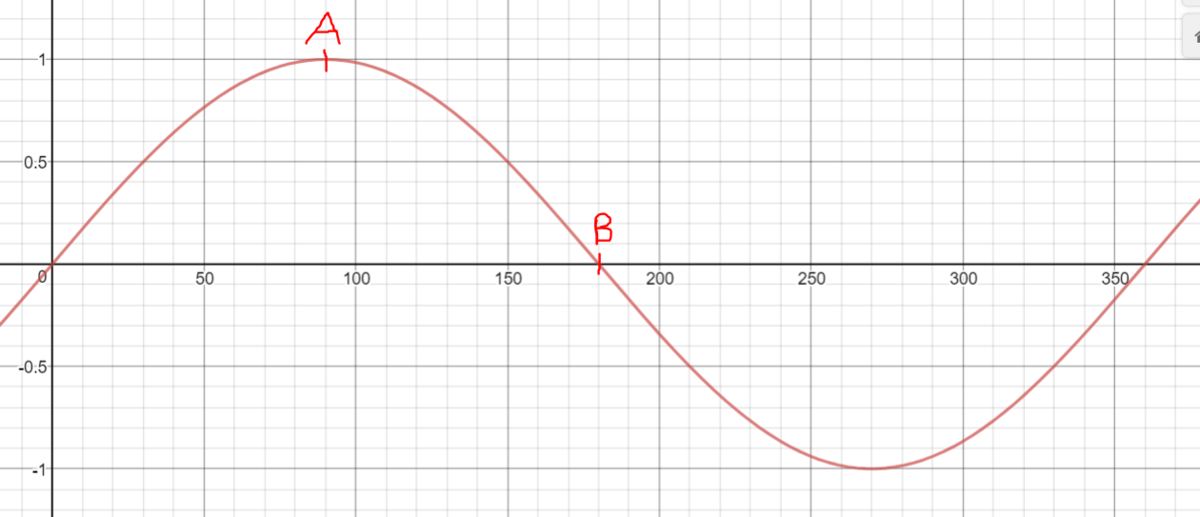

If we shift one of the three values all the way to point B, we get $90+90+180 = 360$ . However, due to the gradient of the function, it is clear that moving towards point B removes more off the value of $\sin x$ , the more that you travel towards B from A. (If this isn't clear, think about the pairs of values of 90 and 180, in comparison to 100 and 170. The difference between 90 and 100 on the y axis is much less than the difference between 170 and 180 on the y axis.)As we want to maximise it, we should move all 3 points together as little as possible, making them all 120. $\implies \text{Maximum} = 3 \cdot \sin 120$ $\text{Maximum} = \frac{3\sqrt{3}}{2}$ $\text{Maximum} = \boxed{2.598}$

Also, notice that using negative values does not help as it is an odd function.