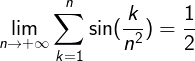This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The formula for the sum of sines in an arithmetic progression gives
k = 1 ∑ n sin ( n 2 k ) = sin ( 2 n 2 1 ) sin ( 2 n 2 n + 1 ) sin ( 2 n 1 )
Multiplying numerator and denominator with n 2 and using lim x → 0 x sin x = 1 , we find a limit of 0 . 5 ( 0 . 5 ) ( 0 . 5 ) = 0 . 5
You can just replace sin ( n 2 k ) by n 2 k , as we have the fact that lim x → 0 x sin x = 1 .
Log in to reply
That step would require a careful justification. You can't just "replace" sin x by x in any limit you see. My strategy is to find the sum first and then "drop the sines" (now the step is easy to justify).
We have: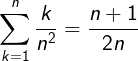
And we can demonstrate that;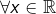 :
:
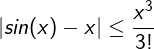
So: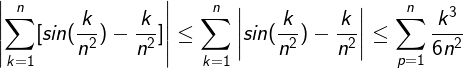
And;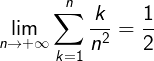
Therfore: