Sum of the reals
x ( x + 1 ) ( x + 2 ) ( x + 3 ) = 1 2 0
Find the sum of all the real roots of the equation above.
The answer is -3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
You could have taken ( x + 3 ) = a and proceeded in a shorter way though.
Log in to reply
Why is the (x+3) before (x+1) as the first equation? Should give you wrong result
Nice skills :D
I'm sorry, I don't understand how you got from the second line to the third.
Log in to reply
I not able to understand second and third line
Nicely done ! I too did the same way but you use to make everthting a perfect square which I skipped by simply checking the discriminant. 😀😀
are negative numbers real numbers?
Log in to reply
Yes they are. But the roots of negative numbers (for instance − 3 9 ) and simplified expressions involving them (for instance − 3 + − 3 9 ) aren't.
Awesome Answer BRO..
Fabulous solution
x(x+1)(x+2)(x+3)=120=(2)(3)(4)(5). Then it's more clear that 2 is one root. Similary, x(x+1)(x+2)(x+3)=(-2)(-3)(-4)(-5). As -5<-4<-3<-2 then -5 is another root. Reducing the equation by Briot-Ruffini Algorithm we obtain (x²+3x+12)(x-2)(x+5)=0. As x²+3x+12 only have imaginary roots, the sum of all real roots is -5+2=-3.
I learned from your post about how the Briot-Ruffini Algorithm is analogous to synthetic division. Nice! :)
This is the easiest solution. Thank you!
I made same
Only 2 solutions possible for this equation,
where x=2 /-5
Hence their sum is, -5+2 = -3
More two are possible, though they will be imaginary. But you can ignore it. So only 2 real solutions are possible. :)
Easier than you thought:
Factorize 120:
1 2 0 = 2 ∗ 3 ∗ 4 ∗ 5
1 2 0 = − 2 ∗ − 3 ∗ − 4 ∗ − 5 .
So x can be either 2 or − 5
Nice observation of factorial 5.
x ( x + 1 ) ( x + 2 ) ( x + 3 ) = 1 2 0 ⇒ x 4 + 6 x 3 + 1 1 x 2 + 6 x − 1 2 0 = 0
Using Lodovico Ferrari’s Method, we can find the roots of this polynomial.
⇒ x = − 5 ∨ 2 ∨ 2 − 3 ± i 3 9
Since two of these roots are real, the answer is: − 5 + 2 = − 3
What is lodovico ferrari's method ?
Let the given equation be p(x) = 120. Then the quartic polynomial p(x) is symmetric in the line x = -1.5, and has roots at x = -3, -2, -1, and 0.
Furthermore, p(x) has the classic "w" shape, featuring
(1) a local maximum at x = -1.5, with p(-1.5) = 9/16;
(2) two global minima, one in (-3, -2) and the other in (-1, 0).
Thus for any k > 9/16, the equation p(x) = k has exactly two real solutions. Since these solutions are symmetric in the line x = -1.5, their sum is -3.
QED
x ( x + 1 ) ( x + 2 ) ( x + 3 ) = 1 2 0
x 4 + 6 x 3 + 1 1 x 2 + 6 x = 1 2 0
x 4 + 6 x 3 + 1 1 x 2 + 6 x − 1 2 0 = 0
( x − 2 ) ( x + 5 ) ( x 2 + 3 x + 1 2 ) = 0
x − 2 = 0
x = 2
x + 5 = 0
x = − 5
− 5 + 2 = − 3
We can ignore the other solutions deriving from x 2 + 3 x + 1 2 = 0 as they include imaginary numbers.
5! = 120
x+3 = 5, x = 2
since there are 4 terms, it wouldn't matter if all of them were negative. by choosing -5 for the first term, we can obtain the same result.
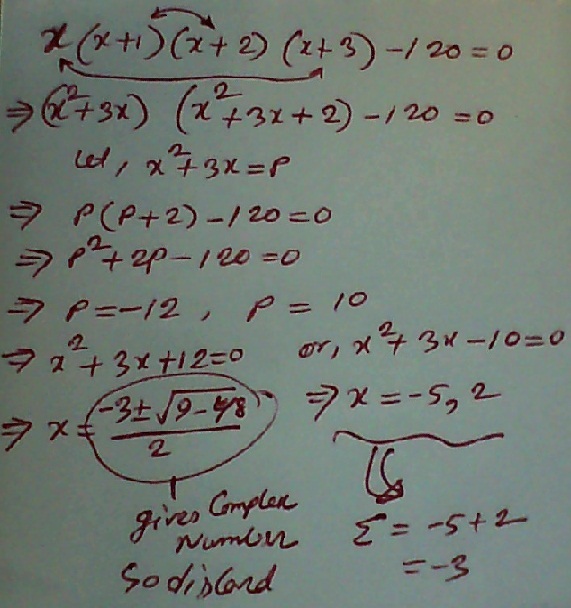
x ( x + 3 ) ( x + 1 ) ( x + 2 ) = 1 2 0
( x 2 + 3 x ) ( x 2 + 3 x + 2 ) = 1 2 0
( x 2 + 3 x ) 2 + 2 ( x 2 + 3 x ) + 1 = 1 2 1
( x 2 + 3 x + 1 ) 2 = ( ± 1 1 ) 2
x 2 + 3 x = − 1 2 o r x 2 + 3 x = 1 0
4 x 2 + 1 2 x = − 4 8 o r 4 x 2 + 1 2 x = 4 0
( 2 x + 3 ) 2 = − 3 9 o r ( 2 x + 3 ) 2 = 4 9
First equation not to be considered (always have imaginary roots)
2 x + 3 = ± 7
x = − 5 , 2