sum of the red angles inside the polygon

Geometry Level 2

What is the sum of the red angles inside the polygon in degrees?

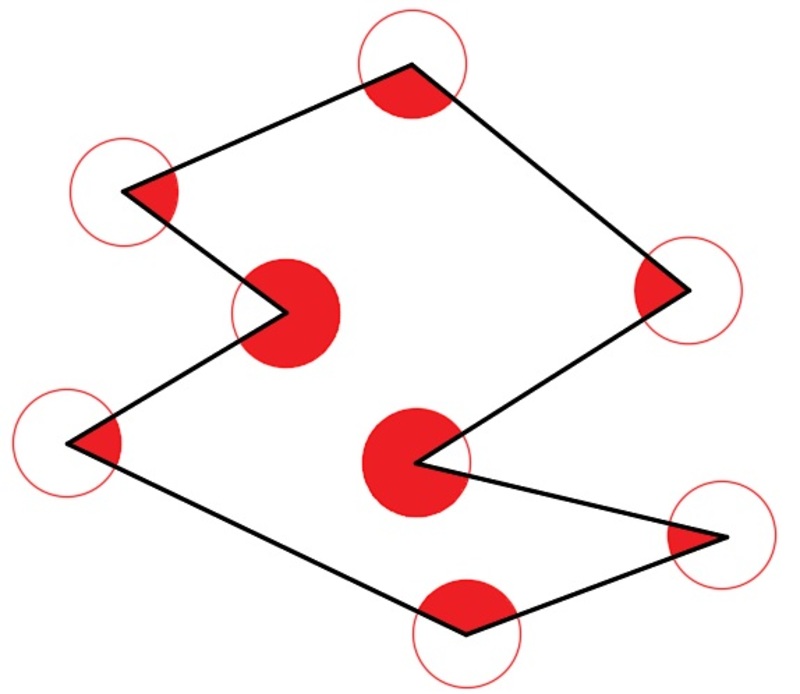
The answer is 1080.

2 solutions

Mahdi Raza
Apr 20, 2020

The diagraram can be split up into three quadrilaterals each of $360^{\circ}$ . Therefore the total angle would be $3 \times 360 = \boxed{1080}$

What software did you use in your diagram?

Marvin Kalngan - 1 year, 1 month ago

Pages, mac application

Mahdi Raza - 1 year, 1 month ago

Kano Boom
Mar 27, 2020

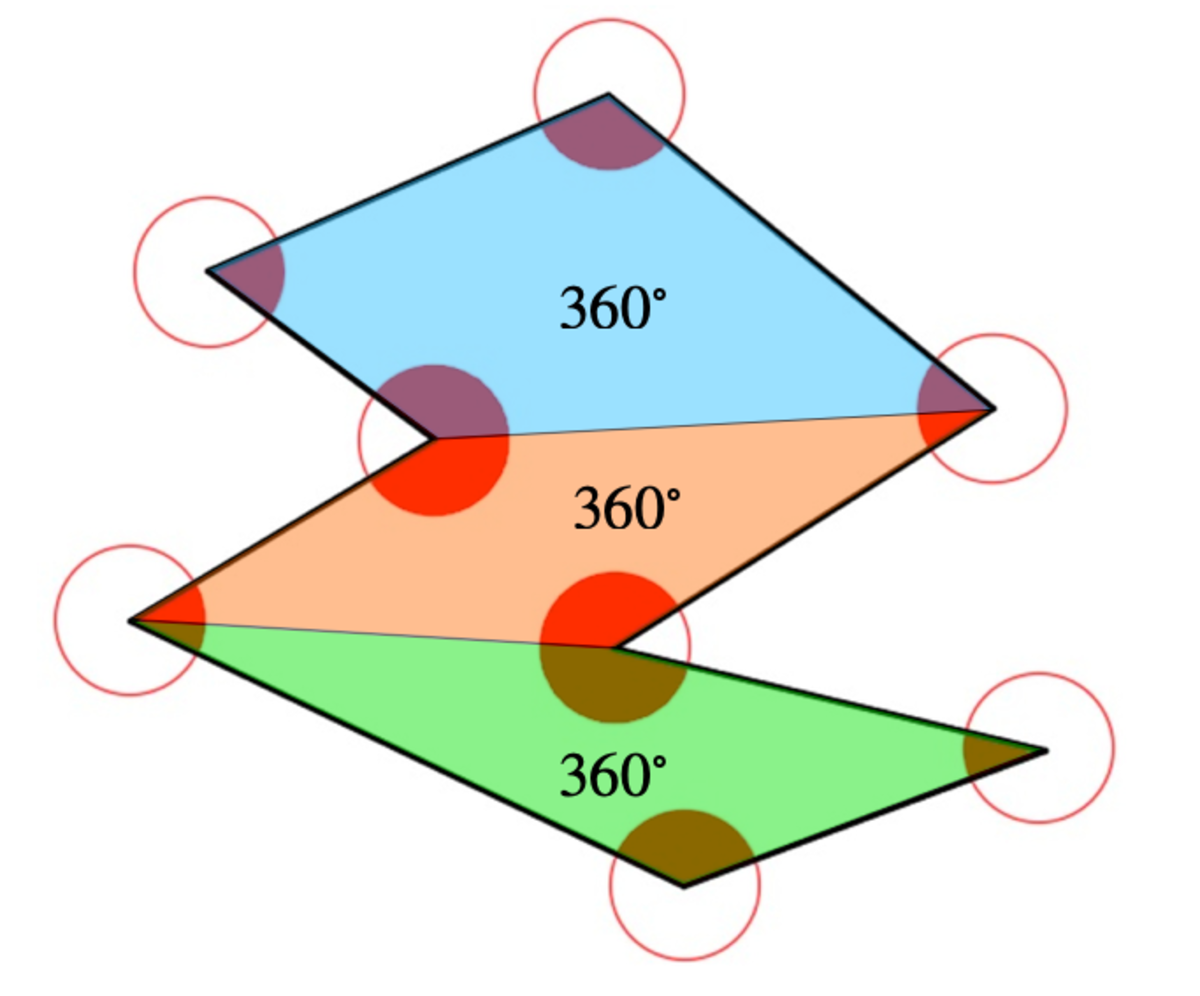
The formula for the sum of all interior angles is $S = (n-2)180^{\circ}$ where $n = # of sides$

Yes, correct.

Marvin Kalngan - 1 year, 2 months ago

What?? If I'm not mistaken, the interior angle sum theorem applies if the polygon is convex. For example, I can construct a six-sided polygon with an interior angle sum of 585 degrees.

Doug Brunson - 1 year, 2 months ago

Nope, it applies to any polygon and can be proven via induction

Kano Boom - 1 year, 2 months ago

I think this problem should be edited.

Doug Brunson - 1 year, 2 months ago

But, Kano, I have a counterexample. 6 sided figure, 540 degrees, not equal to (6-2)*180. I don't know yet how to attach photos. But believe me, you can do it with 2 90 degree angles, two 45 angles, and two 135 angles.

Doug Brunson - 1 year, 2 months ago

https://www.mathsisfun.com/geometry/interior-angles-polygons.html A lot of mathematicans have agreed that this formula is true for any polygon, so therefore it must be true right? Your argument is silly as I could say '6 sided figure, angle sum is 70 degs. With 5 10 degree angles and 1 20 degrees angle

Kano Boom - 1 year, 2 months ago

The website you directed to me is all about convex polygons (regular polygons are a subset of convex polygons). So, I'm correct. To disprove something, it just takes one counterexample.

Doug Brunson - 1 year, 2 months ago

sum of the red angles inside the polygon

The answer is 1080.

2 solutions

0 pending reports