This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
x=3-y => z+3-y=4 => z=4-3+y = 1+y
y + 1 + y = 5 so y=2 x=1 z=3
add them up to get 6 :)
A: x+y=3
B: y+z=5
C: z+x=4
Def A for x: x=3-y
A in C: z+(3-y)=4
z=1+y
Def B for y: y=5-z
To equations with to unknown:
1: z=1+y
2: y=5-z
2 in 1: z=1+(5-z)
z=3
z=3 in 2: y=5-3
y=2
y=2 in A to find x: x=3-2
x=1
Answer: x+y+z=
1+2+3=**6**
There'S a much simpler, 5 second answer: add all 3 equations, to get 2x + 2y +2z = 12, hence the answer is 6.
Actually Jonas it is correct but a long method, to sum up the equations is a precise method
So simple.
x+y=3,
y+z=5,
z+x=4,
So,
x+y+y+z+z+x=3+5+4.
2(x+y+z)=12.
x+y+z=12/2=6
By adding the equations, we get
2(x+y+z)=12
Therefore,
x+y+z=6
Simply..... x+y+y+z+z+x=3+4+5 => 2(x+y+z) = 12 .'. x+y+z = 6 .
Consider the last equation, z + x = 4. If we assume here that neither z or x are zero, then either z = 3 and x = 1 or vice versa. But if z = 1, then y must be 4 since z + y = 5. This is impossible, because then x + y would be 7, but it says here that x + y = 3. So now we only have one value for z and x: z = 3 and x = 1. If x = 1, then y = 2 since x + y = 3.
x = 1, y = 2, and z = 3.
1 + 2 + 3 = 6.
solving the system of equations we get,x=1,y=2,z=3 so the sum is 6
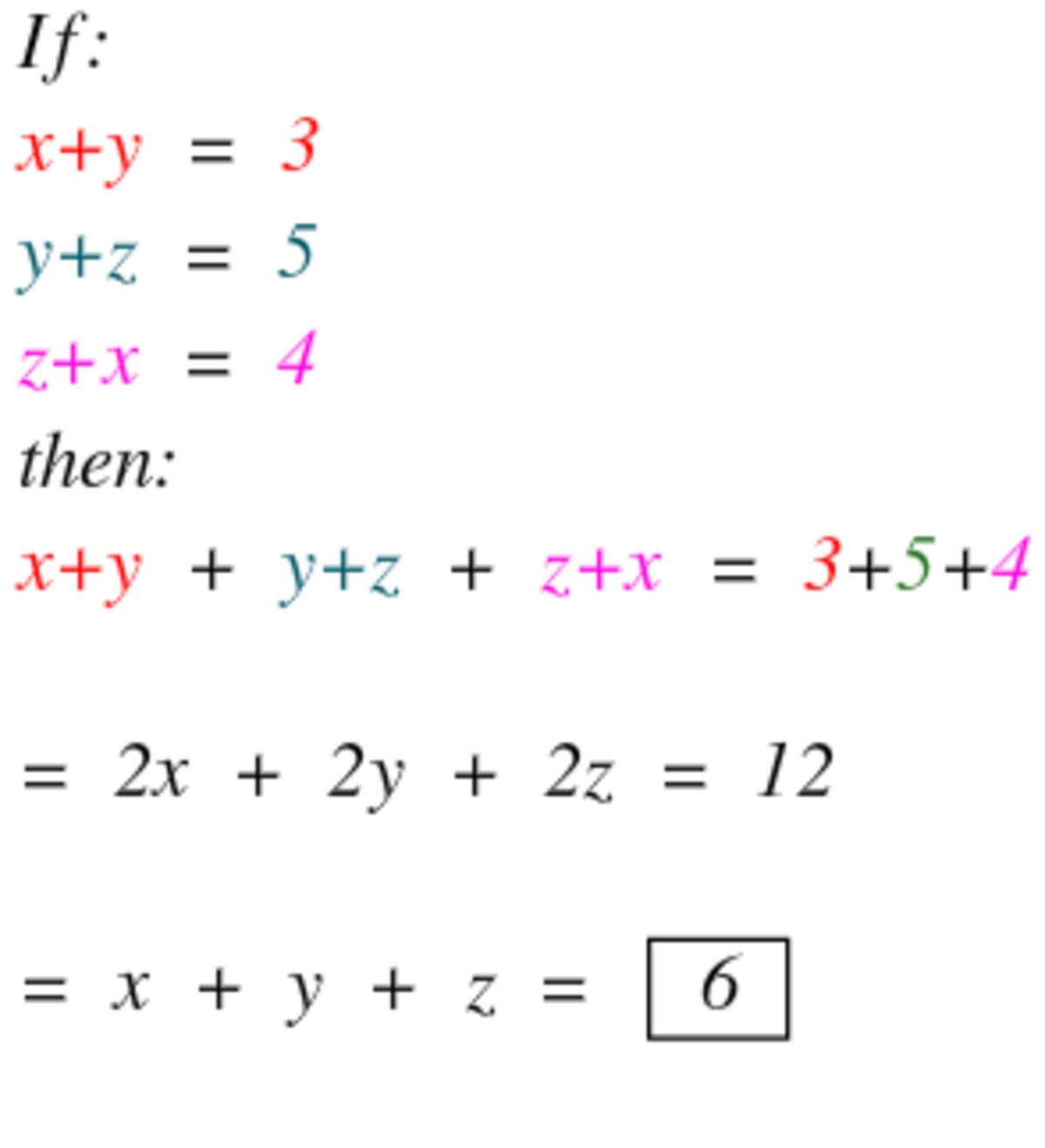
You only need to sum up the three equations, which produces 2 ( x + y + z ) = 1 2 , thus x + y + z = 6 . More precisely, ( x , y , z ) = ( 1 , 2 , 3 )