Sum One

Algebra Level 2

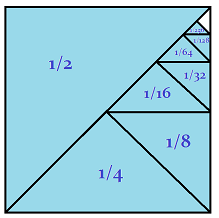
What does this picture best illustrate?

∏ n = 0 ∞ 1 2 n = 1 \prod_{n = 0}^{\infty}\frac{1}{2^n} = 1 ∑ n = 1 ∞ 1 2 n = 1 \sum_{n = 1}^{\infty}\frac{1}{2^n} = 1 ∑ n = 1 ∞ 1 n 2 = 1 \sum_{n = 1}^{\infty}\frac{1}{n^2} = 1 ∑ n = 0 ∞ 1 2 n = 1 \sum_{n = 0}^{\infty}\frac{1}{2^n} = 1 ∑ n = 0 ∞ 1 n 2 = 1 \sum_{n = 0}^{\infty}\frac{1}{n^2} = 1 ∏ n = 1 ∞ 1 2 n = 1 \prod_{n = 1}^{\infty}\frac{1}{2^n} = 1 ∏ n = 1 ∞ 1 n 2 = 1 \prod_{n = 1}^{\infty}\frac{1}{n^2} = 1 ∏ n = 0 ∞ 1 n 2 = 1 \prod_{n = 0}^{\infty}\frac{1}{n^2} = 1

Geoff Pilling by Geoff Pilling , 53, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Geoff Pilling
Mar 16, 2017

The picture shows that if you keep dividing the remaining area in half, and adding it to the previous total you eventually (at ∞ \infty ) get unity represented by the complete square, or ∑ n = 1 ∞ 1 2 n = 1 \boxed{\sum_{n = 1}^{\infty}\frac{1}{2^n} = 1}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...