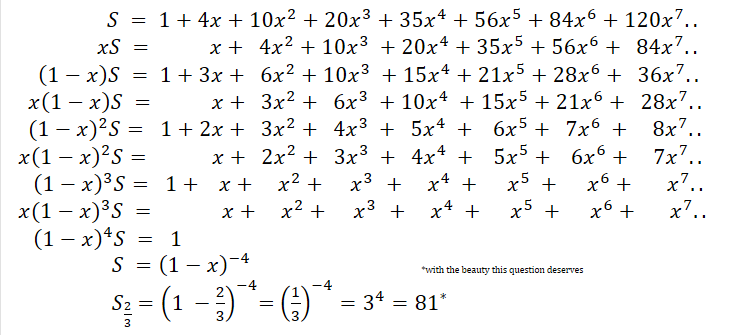Sum to infinity (3)
1 + 4 x + 1 0 x 2 + 2 0 x 3 + 3 5 x 4 + 5 6 x 5 + 8 4 x 6 + 1 2 0 x 7 + ⋯
Given that the n th term after 1 in the sum above is of the form
n ! 4 ⋅ 5 ⋅ 6 ⋯ ( 4 + ( n − 1 ) ) x n .
Evaluate the sum at x = 3 2 .
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This is the series expansion of ( − x + 1 ) 4 1 , so plugging in x = 3 2 gets us 8 1
isn't it ( 1 − x ) 4 1 ?
Log in to reply
what? (looking around...)
This is the series expansion of ( − x + 1 ) 4 1
How do you know this?
Log in to reply
we can see that the general term is
( 3 3 + n ) x n
the expansion of is ( a + b ) − n = k = 0 ∑ ∞ ( − 1 ) k ( k n − 1 + k ) b k a − n − k
here let a = 1 , b = − x and n = 4 to get required sum
The series expansion for ( 1 − x ) n 1 for integer n > 0 happens to be
( 1 − x ) n 1 = k = 0 ∑ ∞ n ! ( n − 1 ) ! ( n + k − 1 ) x k
Compare this with the series expression given in this problem.
Also see Anirudh's comment.
∑ i = 0 ∞ ( i 3 + i ) x i is ( x − 1 ) 4 1 .
3 4 is 8 1 .
The numbers 1, 4, 10, 20, 35 and so on ..... are Tetrahedral numbers
The Generating function for Tetrahedral numbers is
x/(1-x)^4 = x + 4x^2 + 10x^3 + 20x^4.... Divide both sides of the above equation by x to get
1/(1-x)^4 = 1 + 4x + 10x^2 + 20x^3....
Substitute the value of x = 2/3 in the above expression to get the Sum at x = 2/3 as 81.