Sum With Four Squares

Some observations: since the integers $a,b,c,d$ are pairwise* coprime, at most one of them is even; so none of them is.

Similarly, assume exactly one of the integers is a multiple of $3$ . Then the other three are not multiples of $3$ , and reducing modulo $3$ shows that we again reach a contradiction. So there are no multiples of $3$ .

We can even do this modulo $5$ : assume that $a$ is a multiple of $5$ . Then $b^2 \equiv c^2+d^2 \pmod5$ . But the quadratic residues modulo $5$ are $0$ , $1$ and $4$ , and none of $b,c,d$ can be a multiple of $5$ ; so our initial assumption was once again wrong, and there are no multiples of $5$ among the four integers.

Multiples of $2$ , $3$ and $5$ aren't allowed. That means the integers must belong to the set $\{1,7,11,13,17,\ldots\}$ , and we can stop searching here; it turns out the smallest possible set $(a,b,c,d)=(1,13,7,11)$ works, with total $\boxed{32}$ .

Incidentally, the next smallest set $(1,17,11,13)$ also satisfies the equation.

If one of the numbers is even, then the other numbers (as distinct pairwise co-prime integers) must be odd, but then the sum of squares with the even number is odd and the sum of the squares without the even number is even. Therefore, none of the numbers can be even, so all of the numbers must be odd.

$a^2 + b^2 = c^2 + d^2$ can be rearranged to $a^2 - c^2 = d^2 - b^2$ . Since the square of any odd number is $1 \pmod {8}$ , $a^2 - c^2$ (and $d^2 - b^2$ ) is divisible by $8$ . $a^2 - c^2 = d^2 - b^2$ can further be rearranged to $(a - c)(a + c) = (d - b)(d + b)$ , and since all the numbers are odd, each factor $a - c$ , $a + c$ , $d - b$ , and $d + b$ must be even.

Therefore, our search is narrowed down to testing multiples of $8$ that can be written as a product of two even numbers in at least two different ways. For example, testing $24$ we can have $2 \cdot 12$ and $4 \cdot 6$ , for $a = 7$ , $c = 5$ , $d = 5$ and $b = 1$ , but unfortunately in this case $c$ and $d$ are not distinct. The table below summarizes the first few possibilities.

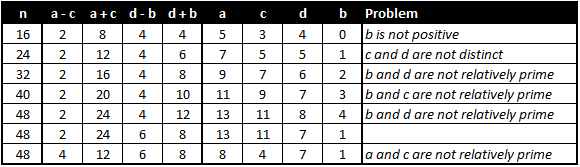
The first number that gives us a correct result is $48 = 2 \cdot 24 = 6 \cdot 8$ , for $a = 13$ , $c = 11$ , $d = 7$ , and $b = 1$ , so that $13^2 + 1^2 = 11^2 + 7^2 = 170$ , which results in the lowest value for $a + b + c + d$ of $13 + 1 + 11 + 7 = \boxed{32}$ .

Chris Lewis' solution is correct.

$\text{Union}\left[a+b+c+d\text{/.}\, \text{Solve}\left[(a|b|c|d)\in \mathbb{Z}_{>\, 0}\land \gcd (a,b)=1\land \gcd (a,c)=1\land \gcd (a,d)=1\land \gcd (b,c)=1\land \gcd (b,d)=1\land \gcd (c,d)=1\land \\ a^2+b^2=c^2+d^2\land a<15\land b<15\land c<15\land d<15\land a\neq b\land a\neq c\land a\neq d\land b\neq c\land b\neq d\land c\neq d\right]\right][[1]] \Rightarrow 32$

Solutions with value less than or equal to 24:

$\left( \begin{array}{cccc} 1 & 13 & 7 & 11 \\ 1 & 13 & 11 & 7 \\ 1 & 17 & 11 & 13 \\ 1 & 17 & 13 & 11 \\ 1 & 23 & 13 & 19 \\ 1 & 23 & 19 & 13 \\ 7 & 11 & 1 & 13 \\ 7 & 11 & 13 & 1 \\ 7 & 19 & 11 & 17 \\ 7 & 19 & 17 & 11 \\ 11 & 7 & 1 & 13 \\ 11 & 7 & 13 & 1 \\ 11 & 13 & 1 & 17 \\ 11 & 13 & 17 & 1 \\ 11 & 17 & 7 & 19 \\ 11 & 17 & 19 & 7 \\ 11 & 23 & 17 & 19 \\ 11 & 23 & 19 & 17 \\ 13 & 1 & 7 & 11 \\ 13 & 1 & 11 & 7 \\ 13 & 11 & 1 & 17 \\ 13 & 11 & 17 & 1 \\ 13 & 19 & 1 & 23 \\ 13 & 19 & 23 & 1 \\ 17 & 1 & 11 & 13 \\ 17 & 1 & 13 & 11 \\ 17 & 11 & 7 & 19 \\ 17 & 11 & 19 & 7 \\ 17 & 19 & 11 & 23 \\ 17 & 19 & 23 & 11 \\ 19 & 7 & 11 & 17 \\ 19 & 7 & 17 & 11 \\ 19 & 13 & 1 & 23 \\ 19 & 13 & 23 & 1 \\ 19 & 17 & 11 & 23 \\ 19 & 17 & 23 & 11 \\ 23 & 1 & 13 & 19 \\ 23 & 1 & 19 & 13 \\ 23 & 11 & 17 & 19 \\ 23 & 11 & 19 & 17 \\ \end{array} \right)$