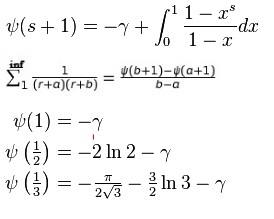Summations can be easy!

Calculus Level 5

$\sum_{n=0}^{\infty}\left( \dfrac{n}{2+\int_{0}^{n} \left(18x^2+26x+9\right)\, dx}\right)= \ln\left(\dfrac{a}{b}\right)-\dfrac{c \pi }{\sqrt{d}}$

$\text{Find:}$ $a+b+c+d+5$ .

Details and Assumptions:

$\bullet$ All the constants in the RHS are positive integers. All fractions are in reduced form (co-prime). $d$ is a square free integer.

This question is part of the set Best of Me .

The answer is 40.00.

2 solutions

Incredible Mind
Jun 25, 2015

all is easy if u know the method...use this and see the magic of digamma

Great job +1!

Samarpit Swain - 5 years, 11 months ago

Tanishq Varshney
Jun 25, 2015

$\displaystyle \sum^{\infty}_{n=0} \frac{n}{6n^3+13n^2+9n+2}$

$\displaystyle \sum^{\infty}_{n=0} \frac{n}{(3n+2)(2n+1)(n+1)}$

Frankly i used wolfram alpha after this step, could u help me after applying partial fraction @Samarpit Swain

@Tanishq Varshney Once you get decompose the sum into $\left(\dfrac{1}{n+1}-\dfrac{1}{n+\dfrac{1}{2}}\right)-2\left(\dfrac{1}{n+1}-\dfrac{1}{n+\dfrac{2}{3}}\right)$

I used the series expansion of $\Psi(x)$ and a few more properties of digamma function to get: $\Psi(1/2)-\gamma-2\Psi(2/3)$ which gives the desired results. I apologize for brevity. I am caught up in a lot of work. I will give the detailed solution along with some of my own generalization soon:)

Samarpit Swain - 5 years, 11 months ago

Summations can be easy!

This question is part of the set Best of Me .

The answer is 40.00.

2 solutions

0 pending reports