Summer solstice
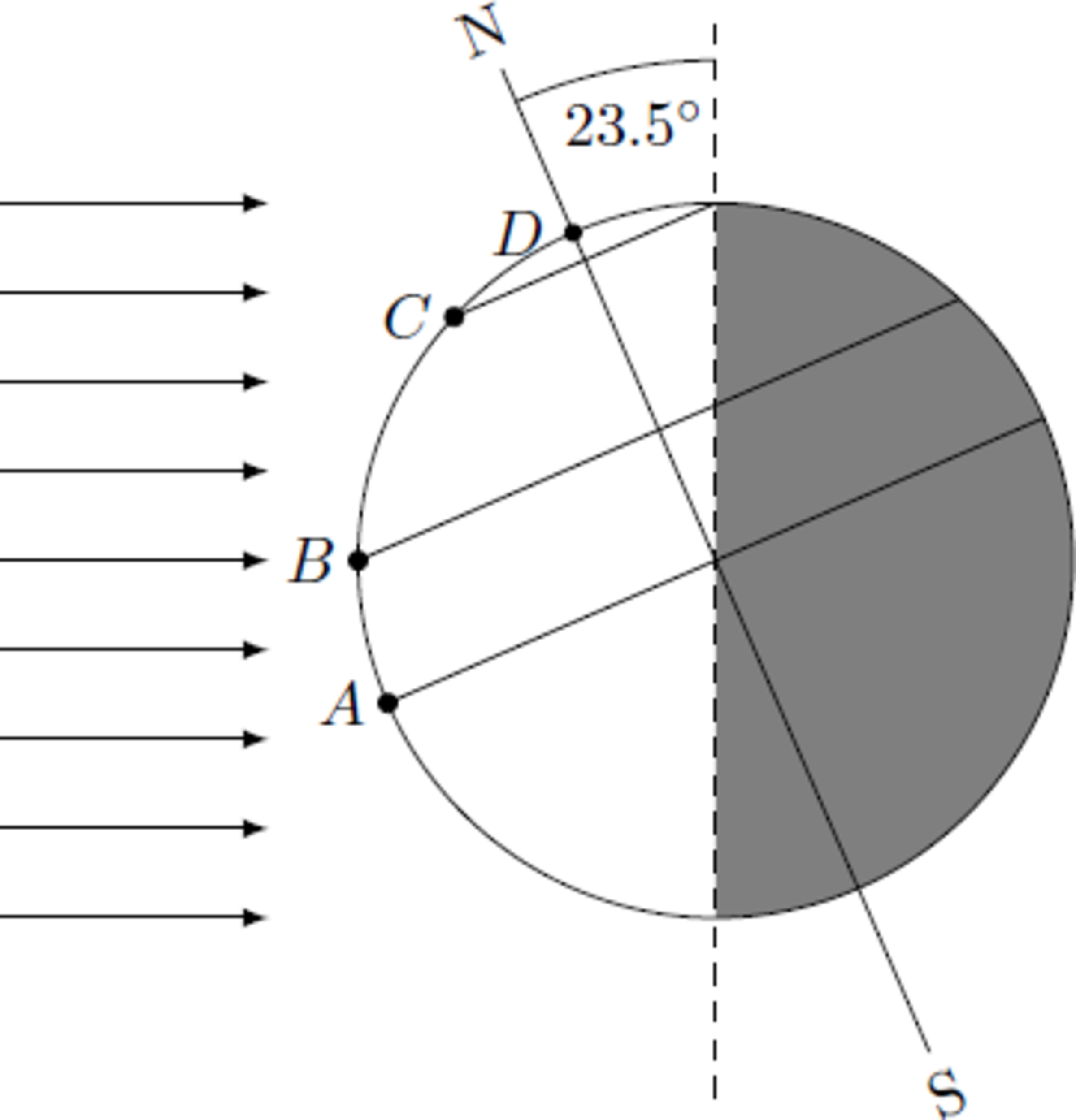
At the summer solstice, the northern hemisphere points towards the sun, so that north of the Arctic Circle (latitude ) the sun does not set. At the northern tropic (latitude ), the midday sun is at its zenith and thus reaches the highest position with an elevation angle .
But which place on earth receives the greatest amount of solar energy at the summer solstice? Here, we consider the solar irradiation per square meter on earth's surface over the entire day. On which latitude lies this place, which receives the largest insulation?
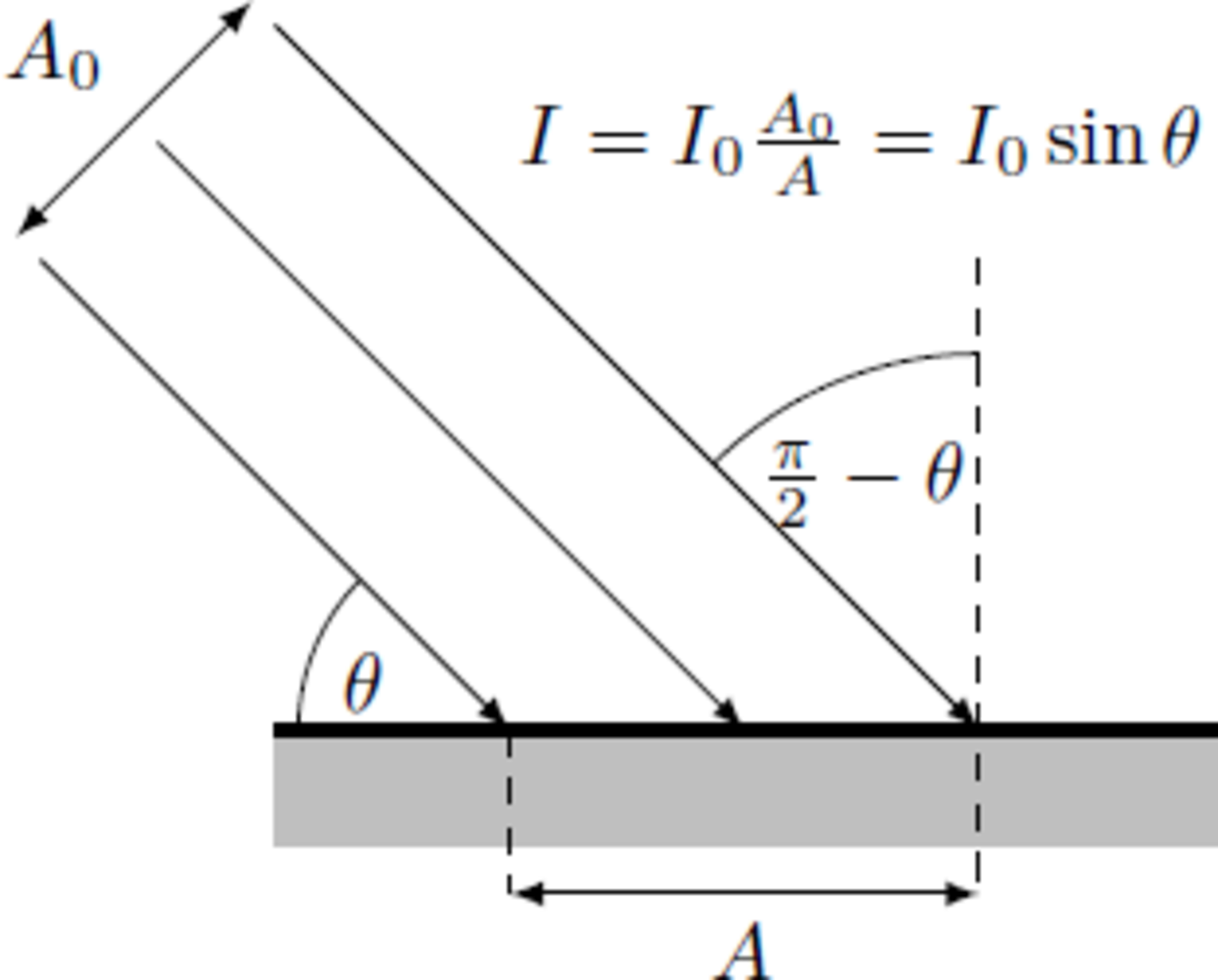
Hints: The sunbeams fall parallel to the earth. The radiation intensity on earth's surface depend on the solar elevation angle , which varies throughout the day due to the rotation of the earth. The total solar irradiation results from integration of the intensity over the complete day. Suppose that the earth corresponds to a perfect sphere whose axis of rotation is tilted by an angle .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A location on the earth's surface is defined by latitude ϕ and longitude λ , so that in the earth-fixed frame of reference this point can be described in spherical coordinates by the vector
r = r E ⎝ ⎛ cos ϕ cos λ cos ϕ sin λ sin ϕ ⎠ ⎞
where r E is the earth radius. Since the longitude is not relevant here, we set λ = 0 . In fact, the earth rotates counterclockwise from east to west with the angular velocity ω = 2 4 h 2 π and is tilted by the angle δ = 2 3 . 5 ∘ towards the ecliptic. In order to get from the earth-fixed vector r to the space-fixed coordinates R , we have to multiply the vector by two rotation matrices R t and D δ which correspond respectively to the rotation and the tilt of the earth:
R = D δ ⋅ R t ⋅ r = ⎝ ⎛ cos δ 0 sin δ 0 1 0 − sin δ 0 cos δ ⎠ ⎞ ⋅ ⎝ ⎛ cos Ω t sin Ω t 0 − sin Ω t cos Ω t 0 0 0 1 ⎠ ⎞ ⋅ r E ⎝ ⎛ cos ϕ 0 sin ϕ ⎠ ⎞ = ⎝ ⎛ cos δ 0 sin δ 0 1 0 − sin δ 0 cos δ ⎠ ⎞ ⋅ r E ⎝ ⎛ cos ϕ cos Ω t cos ϕ sin Ω t sin ϕ ⎠ ⎞ = r E ⎝ ⎛ cos δ cos ϕ cos Ω t − sin δ sin ϕ cos ϕ sin Ω t sin δ cos ϕ cos Ω t + cos δ sin ϕ ⎠ ⎞
As connection vector between earth and sun we choose S = − a e X in negative X direction, so that the elevation of the sun is highest at midday t = 1 2 h . Since the position vector R is perpendicular to the Earth's surface, the angle between the vectors S and R is just the angle of incidence of the Sun's rays:
⇒ ⇒ ∠ ( S , R ) ∣ S ∣ ∣ R ∣ S ⋅ R θ = 2 π − θ = sin δ sin ϕ − cos δ cos ϕ cos Ω t = cos ( 2 π − θ ) = sin θ = arcsin ( sin δ sin ϕ − cos δ cos ϕ cos Ω t )
Negative elevation angles θ < 0 occur at night while during the day is θ > 0 . The times for sunrise and sunset are then given by the condition θ = 0 :
t sunrise t sunfall = { Ω 1 arccos ( tan δ tan ϕ ) 0 ϕ < 2 π − δ ϕ ≥ 2 π − δ = Ω 2 π − t sunrise
Here, the latitude ϕ = 2 π − δ = 6 6 . 5 ∘ corresponds to the Arctic Circle, so that the sun rises at midnight and there is no night. The temporal course of the sun's position θ ( t ) is sketched in the diagram below. At the tropic ( ϕ = δ ) the curve θ ( t ) corresponds to a triangular function with a maximum at θ = 2 π = 9 0 ∘ . At the North Pole, on the other hand, the position of the sun is constant with θ = δ = 2 3 . 5 ∘ .
We can already exclude the answer option ϕ = 0 (equator), because according to the diagram the elevation of the sun is always larger at the tropic than at the equator ( θ ϕ = δ > θ ϕ = 0 ). For all other cases, the total incidence of light will have to be calculated by integration:
I tot I tot = I 0 ∫ t sunrise t sunfall sin θ ( t ) d t = I 0 ∫ t sunrise t sunfall ( sin δ sin ϕ − cos δ cos ϕ cos Ω t ) d t = I 0 ( sin δ sin ϕ ( t sunfall − t sunrise ) − Ω cos δ cos ϕ ( sin t sunfall − sin t sunrise ) ) = I 0 ⋅ 2 4 h × ⎩ ⎪ ⎨ ⎪ ⎧ ≈ 0 . 3 5 2 cos ( δ ) sin ( δ ) ≈ 0 . 3 6 6 sin ( δ ) ≈ 0 . 3 9 9 ϕ = 2 3 . 5 ∘ ( case B ) ϕ = 6 6 . 5 ∘ ( case C ) ϕ = 9 0 ∘ ( case D )
In fact, the solar irradiation at the North Pole reaches the highest value. Plotting the whole function I tot ( ϕ ) also shows that this is the global maximum of the curve. Nevertheless, it is not really warm at the North Pole even at the summer solstice. Firstly, there is a high sun intensity only for a very short time period at the North Pole, so that the place has no time to warm up. In addition, the albedo of snow and ice is particularly high, so that the majority of the incident sunlight is directly reflected and does not contribute to the increase in temperature. Nevertheless, one should not forget the sunscreen at a North Pole expedition in summer.