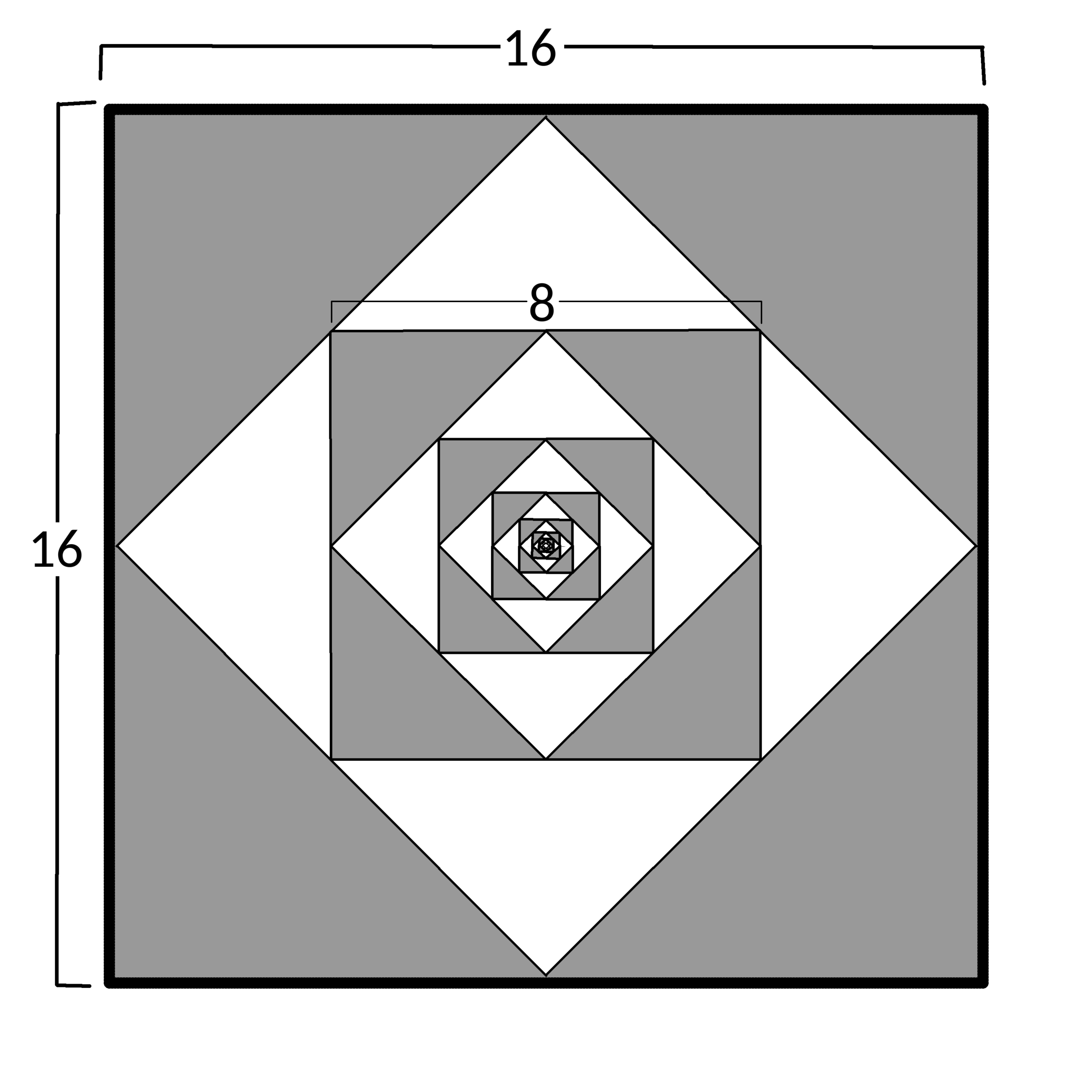
Summing areas of triangles

Area of the 4 triangles is half the area of the square for all squares and area of inner square is half the area of the outer square

So $Shaded - Unshaded=A(\frac{1}{2}-\frac{1}{2}*\frac{1}{2}+\frac{1}{2}*\frac{1}{2}*\frac{1}{2}-\frac{1}{2}*\frac{1}{2}*\frac{1}{2}*\frac{1}{2}...$ where $A=256$ is the are of outermost square.

This is a G.P with common ratio $-\frac{1}{2}$ and its sum can be calculated to be $\frac{A}{3}$

Thus our answer is 256+3=259

The area of the shaded region can be found by calculating $\sum _{ n=0 }^{ \infty }{ \frac { 128 }{ { 4 }^{ n } } }$ . The area of the non-shaded region is $\sum _{ n=0 }^{ \infty }{ \frac { 64 }{ { 4 }^{ n } } }$ . Thus $\sum _{ n=0 }^{ \infty }{ \frac { 128 }{ { 4 }^{ n } } } -\sum _{ n=0 }^{ \infty }{ \frac { 64 }{ { 4 }^{ n } } } =\frac { 256 }{ 3 }$ $a+b=256+3=\boxed { 259 }$